4. WEATHER

Meteorological data used as input for WOFOST/CGMS are: maximum temperature (°C),  minimum temperature  (°C), CGMS: mean daily vapour pressure (hPa) Wofost: early morning vapour pressure (kPa) , rainfall (mm) and mean daily windspeed at 2m. These data are retrieved from the Global Telecommunication System (GTS) of the World Meteorological Organisation (WMO). In addition, WOFOST/CGMS needs global  radiation (J.m^-2.d^-1) as input. This information is rarely broadcast over the GTS and is estimated from other meteorological parameters. Methods and weather variables used to estimate daily values of global radiation are described in Subsection 4.1.2. Windspeed observations obtained from the GTS are registered at a 10 m height and should therefore be transformed with the logarithmic transformation method to  windspeed at 2 m.

The above mentioned meteorological variables, as well as the estimated global radiation and evapotranspiration according to Penman are processed at station level and subsequently interpolated to a grid. For operational use the European Commission applies a grid size of 50*50km for member states of the European Union (EU). However, for instalations on country level other grid sizes can be applied. (For example the CGMS installation in the Czech Republic applies a 10*10km grid). Variables of the final product on Level 1 are depicted in Table 4.1.
 

Table 4.1. Meteorological variables that are interpolated to the grid center (50 x 50 km or 10 x 10 km)
 

Variable	Description
Tmax	maximum temperature (°C)
Tmin	minimum temperature (° C)
ea	mean daily vapour pressure (hPa) (for CGMS) early morning vapour pressure (kPa) (for stand alone Wofost)
u(10)	mean daily windspeed at 10m (m.s-1)
RAINFALL	mean daily rainfall (mm)
E0	Penman potential evaporation from a free water surface (mm/day). See Section 4.1.
ES0	Penman potential evaporation from a moist bare soil surface (mm.d-1). See Section 4.1.
ET0	Penman potential transpiration from a crop canopy (mm/day). See Section 4.1.
Rg,d	daily global radiation in KJ.m-2d-1

The interpolation method applied is described in Section 4.3. It is important to realise that these values are used to describe the "average" conditions prevalent in the grid cell for a particular day. They do not necessarily represent the meteorological conditions that could be measured at the grid cell center. The applied altitude variable describes the mean altitude of agricultural activity in the grid cell it does not represent the altitude that can be measured at the grid cell center.

Subroutine Penman calculates the potential evapotranspiration of a crop canopy, bare soil and a water surface. Some intermediate variables, used in the calculation are also computed.
 
 

4.1. Calculation of evapotranspiration

The term evapotranspiration covers both transpiration and evaporation. Strictly speaking, transpiration is water loss from plants and evaporation is water loss from soil or a free-water surface. The main driving force for evaporation is the gradient of vapour pressure between the evaporating surface and surrounding air. Vapour pressure at the evaporating surface is equal to the saturated vapour pressure at the prevailing temperature of that surface. Vapour pressure of air is a function of ambient temperature and its relative humidity. The evaporation rate depends on the diffusion resistance between the evaporating surface and the air. The magnitude of this resistance is strongly related to wind speed. The two environmental variables, air humidity and wind speed combined determine the 'evaporative demand' of the air.

The problem in the approach above is that temperature of the evaporating surface is usually not known from standard meteorological observations. Evaporation of 1 mm layer of water requires 2.4 MJ m^-2 and can therefore be described through quantification of an energy balance. The energy dissipation required for evaporation, leads to cooling of the evaporating surface, which reduces the vapour gradient. Hence, a driving force is required to maintain the corresponding surface temperature, and thus, maintain the vapour pressure gradient. The energy for this driving force is supplied by the net solar radiation received by canopy and or soil.

Net radiation is the balance between incoming (short-wave) radiation from the sun and radiation losses due to reflection and outgoing (long-wave) radiation. Heat supplied by moving air is another source of energy, but this is usually negligible, except in situations where the vegetation is surrounded by extensive bare areas (oasis). Only 5-8% of incoming radiation is dissipated in photosynthesis, which is, therefore, disregarded here. Respiration yields an insignificant amount of energy. To simplify the treatment of evapotranspiration, it is considered to be governed by two factors: radiation and evaporative demand.

Penman (1948) was the first to describe evapotranspiration in physical mathematical terms. He calculated evaporation from free-water surfaces, wet bare soil and low grass swards for 10-day periods. There is no consensus whether the Penman formulae are also applicable for 1 day periods. If the Penman equation is used to estimate ith daily values, 24 hour average values should be used as input. For large day/night differences (e.g. in wind speed), Doorenbos & Kassam (1979) suggested the use of correction factors.

The value calculated according to the Penman equations is the potential evapotranspiration, i.e. without limitations with respect to the supply of liquid water to the evaporating surface. This ET0 (Penman) value is often used as a reference value, to which actual crop water demand is related. To translate ET0 into crop water requirements, so called crop factors can be used (e.g. Doorenbos & Pruitt, 1977; Feddes et al., 1978).

The Penman formula (equation 4.1) consists of two segments. The first part, the radiative term, calculates the net absorbed radiation. The second part, the aerodynamic term, calculates the evaporative demand of the atmosphere (Choisnel et al., 1992; Frère & Popov, 1979; Penman, 1956, 1948). The resulting equations are used to calculate the potential evaporation rates from a water surface, from bare soil surfaces and the potential evapotranspiration rate from a crop canopy.

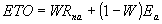(4.1)

where	ET0	:	Evapo(transpi)ration	[mm d-1]
	W	:	Temperature related weighing factor	[-]
	Rna	:	Net absorbed radiation in equivalent evaporation	[mm d-1]
	EA	:	Evaporative demand in equivalent evaporation	[mm d-1]

 

4.1.1. Preparatory calculations

The average temperature is calculated as the average of the minimum and the maximum temperature. This average temperature is equal to the so called air temperature (T) used in the model calculations. The maximum and minimum temperature are measured daily values.

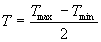(4.2)

where	T	:	Average daily air temperature	[°C]
	Tmax	:	Maximum temperature	[°C]
	Tmin	:	Minimum temperature	[°C]

The difference between maximum and minimum temperature is used to calculate the empiric constant of the wind function in the Penman equation.

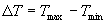(4.3)

where	DT	:	Temperature difference	[°C]
	Tmax	:	Maximum temperature	[°C]
	Tmin	:	Minimum temperature	[°C]

As will be explained in  Subsection 4.1.3, the evaporative demand, EA, depends on the windspeed and the difference between saturated and actual vapour pressure. The windspeed dependency is incorporated in the evaporative demand as the windspeed measured at a height of two meters, and multiplied by an empirical coefficient. This coefficient is temperature dependent and can be calculated as (Frère, 1979):

	for	(4.4a)
	for	(4.4b)

where	BU	:	Empirical coefficient in the wind function	[-]
	DT	:	Temperature difference	[°C]

Air temperature can be used to calculate the latent heat of vaporization:

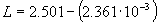(4.5)

where	L	:	Latent heat of vaporization	[J kg-1]
	T	:	Average daily temperature	[°C]

As the value of the latent heat varies only slightly over normal temperature ranges a single value for L can be applied. In WOFOST/CGMS for L a value of 2.45 10⁶ J kg^-1 is assumed (T=20°C). The psychrometric constant  at sea level is calculated as follows (Brunt, 1932):

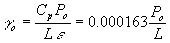(4.6)

where	go	:	Psychrometric constant at sea level	[hPa °C-1]
	Cp	:	Specific heat of moist air =1013	[J kg-1 °C-1]
	Po	:	Atmospheric pressure at sea level	[hPa]
	e	:	Ratio molecule weight water vapour / dry air = 0.622
	L	:	Latent Heat of vaporization = 2.45 106	[J kg-1]

In WOFOST/CGMS however, a fixed value of g_o = 0.67 mbar°C^-1 is assumed, assuming that the atmospheric pressure at sea level P_o is constant at 1013 hPa. It should be mentioned, that the barometric pressure changes with altitude, so does also the psychrometer constant. Therefore, the two following equations are used to correct for altitude difference.

img src="uploads/weather/eq4-7.gif">

(4.7)

where	P	:	Atmospheric pressure at elevation z	[hPa]
	Po	:	Atmospheric pressure at sea level	[hPa]
	T	:	Daily temperature	[°C]
	z	:	Elevation	[m]

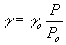(4.8)

where	g	:	Psychrometric constant at elevation z	[hPa °C-1]
	go	:	Psychrometric constant at sea level	[hPa °C-1]
	P	:	Atmospheric pressure at elevation z	[hPa]
	Po	:	Atmospheric pressure at sea level	[hPa]

Saturated vapour pressure is related to mean daily air temperature and may be approximated with (Goudriaan, 1977):

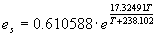(4.9)

where	es	:	Saturated vapour pressure	[hPa]
	T	:	Air temperature	[°C]

From this equation the derivate, i.e. the slope of the saturated vapour pressure-temperature curve is established.

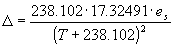(4.10)

where	D	:	Slope of the saturation vapour pressure curve	[hPa °C-1]
	es	:	Saturated vapour pressure	[hPa]
	T	:	Air temperature	[°C]

In WOFOST/CGMS the measured vapour pressure is not allowed to exceed the calculated saturated vapour pressure.
 
 

4.1.2. Methods to estimate global radiation applied in WOFOST/CGMS

Solar radiation provides the energy for photosynthesis and transpiration of crops and is one of the meteorological factors determining potential yield. However, daily measurements of solar radiation are far too scarce and dispersed for operational use in crop growth simulation models. Test on data received via the GTS for the first six months of 1997 revealed that none of the 1200 recording stations which information is used in WOFOST/CGMS had reported global radiation. Various alternatives exist to solve this problem:

• the use of average values,
• spatial interpolation,
• estimation global radiation values from remote sensing data or
• estimation of these values from other climatic variables.

Nonhebel (1993) studied the consequences of using average values in a crop growth simulation model. She concluded:." Due to the variation in daily and annual global radiation and the nonlinear relation between radiation and photosynthesis, the use of average data (even over short periods) to replace missing data must be avoided."

Spatial interpolation is not always an option since the density of recording stations is too sparse in various regions in Europe and Northern Africa. According to Hubbard (1994), to account for more than 90% of the spatial variation in global radiation in the high plains of the USA, distance between the observing station and the location for which the value has to be interpolated, should be less than 30 km.

Iehlé et al. (1997) reviewed various methods to retrieve global radiation from satellite data. They concluded that although the results were promising, the quality of the estimates was not sufficient for operational use.

 Alternatively, global radiation may be estimated from other climatic variables such as sunshine duration (Boisvert et al., 1990; Soler, 1990; Rietveld, 1978; Ångström, 1924); air temperature range (De Jong & Stewart, 1993; Hargreaves et al., 1985; Bristow & Campbell, 1984), precipitation (De Jong & Stewart, 1993) and cloud-cover (Barker, 1992; Davies & McKay, 1988; Brinsfield et al., 1984). Whenever possible, in CGMS the equation postulated by Ångström (1924) and modified by Prescott (1940) to its present form is applied:

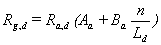(4.11)

where	Rg,d	:	Incoming daily global solar radiation	[J m-2 d-1]
	Ra,d	:	Daily extra-terrestrial radiation (see eq. 4.26)	[J m-2 d-1]
	Aa	:	Empirical constant	[-]
	Ba	:	Empirical constant	[-]
	n	:	Bright sunshine hours per day	[hr]
	Ld	:	Astronomical day length (see eq. 4.24)	[hr]

The regression constants A_a and B_a have a physical meaning: A can be considered as the fraction of extra terrestrial radiation on overcast days. Sum of A_a and B_a can be considered as the fraction of radiation received on clear days. For several regions in Europe, the Middle East and Northern Africa  the Ångström-Prescott constants have been established by Supit (1994), Supit & van Kappel (1998) and van Kappel & Supit (1998). (See Appendix I)

Provided that values of the constants are available, the Ångström-Prescott method is easy to apply. However, for many locations daily sunshine duration is not observed or irregularly broadcasted via GTS, and therefore the Ångström method, or any other method applying sunshine duration (e.g. Soler, 1990), is not always applicable. Therefore, in WOFOST/CGMS when sunshine duration observations are not available the following equation that uses cloud cover observations and the temperature range as input  is applied  (Supit, 1994; Supit van Kappel 1998):

(4.12)

where	Rg,d	:	Incoming daily global solar radiation	[J m-2 d-1]
	Ra,d	:	Daily extra-terrestrial radiation (see eq. 4.26)	[J m-2 d-1]
	CC	:	Mean total cloud cover during daytime	[octas]
	Tmax	:	Maximum temperature	[°C]
	Tmin	:	Minimum temperature	[°C]
	As	:	Empirical constant	[°C-0.5]
	Bs	:	Empirical constant	[-]
	Cs	:	Empirical constant	[J m-2 d-1]

Clouds and their accompanying weather patterns are among the most important atmospheric phenomena restricting the availability of solar radiation at the earth. s surface. Various studies to estimate global solar radiation from observations of various cloud layer amounts and cloud types have been executed (e.g. Barker, 1992; Davies & McKay, 1988). Most of the models proposed in these studies require detailed knowledge of local hourly sums of direct and diffuse radiation for clear skies as well as hourly cloud cover observations (Brinsfield et al., 1984). Since this information is not available on GTS, these models cannot be considered as an alternative for estimation of daily global radiation.

The above mentioned method (a.k.a the extended Hargreaves or the Supit method in the software code), is  slightly less accurate in comparison to the results obtained with the Ångström formula. Constants A_s, B_s and C_s for various regions in Europe, the Middle East and Northern Africa have been established by Supit (1994), Supit & van Kappel (1998) and van Kappel & Supit (1998) (See Appendix I)

When neither sunshine duration nor cloud cover observations are available, the Hargreaves formula (1985) will be applied. The accuracy of this method is less then the accuracy of the two earlier mentioned methods.

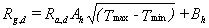(4.13)

where	Rg,d	:	Incoming daily global solar radiation	[J m-2 d-1]
	Ra,d	:	Daily extra-terrestrial radiation (see eq. 4.26)	[J m-2 d-1]
	Tmax	:	Maximum temperature	[°C]
	Tmin	:	Minimum temperature	[°C]
	Ah	:	Empirical regression constants	[°C-0.5]]
	Bh	:	Empirical regression constants	[J m-2 d-1]

Constants A_h and B_h for various regions in Europe, the Middle East and Northern Africa have been established by Supit (1994), Supit & van Kappel (1997) and van Kappel & Supit (1998) (See Appendix I). In Section 4.2 calculation of the daily extra-terrestrial radiation, R_a,d, is explained . In subroutine CalcAddWeather  the algorithms discussed in this subsection are applied.
 
 

4.1.3. Estimation and interpolation of the regression constants

Quality of the radiation estimates obtained with equations (4.11), (4.12) and (4.13) depend on the quality of the data used to establish these regression constants. Supit (1994) showed that in many cases there is no relation between the latitude and the coefficients, although such a relation is frequently used to estimate these regression constants.

The main purpose of the work by Supit (1994) and Supit & van Kappel (1997) has been to obtain sets of regression constants for the above mentioned formulae for as many weather stations as possible, with a geographic distribution that corresponds to the area of interest for CGMS. As a result, a set of 256 reference stations has been identified for which a relevant set of measured radiation data and other parameters in the formulae exist. For these stations the regression constants have been calculated based on measured radiation data for the three formulae mentioned above. See Appendix I for the yearly Ångström-Prescott, the extended Hargreaves (or the Supit) and for the Hargreaves constants.

Based on the latitude, longitude, altitude and the regression constants calculated of the reference stations, the regression constants for the stations used for the interpolation of the daily meteorological data are derived. This is a process that only has to be carried out once, unless the set of reference stations changes. Once the regression constants have been established for the operational set of stations, the global radiation estimation can proceed using any one of the above formulae.

The interpolation of the regression constants is based on a simple distance weighted average of the three nearest stations (van der Goot, 1997). For each of the three sets of constants (Ångström, Supit, Hargreaves) a subset is created from the complete set of reference stations, by selecting only those stations that have the regression coefficients for the desired method. This subset of stations is then sorted based on distance to the station for which the regression coefficients are being calculated. This sorting process is also subject to an altitude threshold test i.e. if the altitude difference between the target station and a reference station is greater than a set threshold the reference station is rejected in favour of the next nearest reference station. Depending on a distance threshold, the nearest one, two or three stations are then used to calculate the regression constants. If the threshold tests exclude all stations, the nearest station will be used, regardless of the distance. The altitude threshold value is 200m, the distance threshold is 200km.

The distance weighted average method used is based on the relative distance of the reference stations to the station of interest. Assume the distances d₀, d₁ and d₂ to be the distances to the three nearest reference stations, and w₀, w₁ and w₂ the weights to be used in the calculation. As an example, assume that d₁ is 2*d₀, then w₁ will be w₀/2. More general, w₁ = w₀*d₀/d₁. Similarly, w₂ = w₀*d₀/d₂. Furthermore, the sum of the weights should be 1, so w₀+w₁+w₂ = 1. From the above, the following relation can be established:

w0 = d1d2 / (d0d1 + d0d2 + d1d2)	(4.14a)
w1 = d0d2 / (d0d1 + d0d2 + d1d2)	(4.14b)
w2 = d0d1 / (d0d1 + d0d2 + d1d2)	(4.14c)

According to van Kappel (not published) the weighted distance interpolation provides the best results when interpolation the constants of the radaiation estimation equations. Note that the maps in Appendix I are obtained with the Kriging method.
 
 

4.1.4. Terms in the Penman formula

The temperature related weighing factor W in equation 4.1 is defined as (Frère and Popov, 1979; Penman, 1948, 1956).

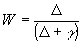(4.15)

where	D	:	Slope of the saturation vapour pressure curve (see eq. 4.10)	[hPa °C-1]
	g	:	Psychrometric constant (see eq. 4.8)	[hPa °C-1]

To calculate net outgoing long wave radiation Penman (1956) used an equation which is derived from the formula postulated by Brunt (1932). The net outgoing long wave radiation increases with increasing values for the mean air temperature and the relative sunshine duration and decreases with increasing vapour pressure.

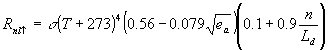(4.16)

where		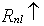:	Net outgoing long-wave radiation	[J m-2 d-1]
	s	:	Stefan Boltzmann constant = 4.90 x 10-3	[J m-2 K-4 s-1]
	T	:	Air temperature	[°C]
	ea	:	Actual vapour pressure	[kPa]
	Be	:	Constant according to Brunt (1932)	[-]
	Bf	:	Constant according to Brunt (1932)	[-]
	n/Ld	:	Relative sunshine duration	[-]

The two Brunt constants B_e and B_f  depend on latitude. In WOFOST/CGMS if latitude is less than 45° the following values are assumed: B_e = 0.3 and B_f  = 0.7. For all other latitudes B_e and B_f  are set to 0.1 and 0.9, respectively. The relative sunshine duration is either taken from the daily meteorological data, or  established using the following equation:

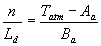(4.17)

where	n/Ld	:	Relative sunshine duration	[-]
	Tatm	:	Atmospheric transmission (i.e.  Rg,d/Ra,d)	[-]
	Aa	:	Empirical constant in the Ångström equation	[-]
	Ba	:	Empirical constant in the Ångström equation	[-]

Part of the actual received radiation is reflected by the surface. The fraction reflected (albedo) is different for a water surface, a soil surface and a crop canopy. The absorbed fraction of radiation actually received minus the net outgoing radiation equals the net absorbed radiation, which is divided by the latent heat of vaporization of water to express the amount of radiation in depth of evaporative water layer (mm d^-1).

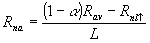(4.18)

where	Rna	:	Net absorbed radiation	[mm d-1]
	a	:	Albedo or reflection coefficient of regarded surface	[-]
	Rav	:	Average radiation	[J m-2 d-1]
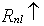		:	Net outgoing long-wave radiation	[J m-2 d-1]
	L	:	Latent heat	[J kg-1]

Either measured or estimated daily global irradiation (wavelength 300-3000 nm) is used as  input in WOFOST/CGMS and furthermore R_av=R_g,d is assumed. Soil albedo depends on the surface color and on the moisture content. Albedo values for dry soil vary from 0.14 (clay) to 0.37 (dune sand). Ten Berge (1986) described the dependence of the albedo value on soil moisture in relation to the average water content of the top soil layer. See Table 4.2. In WOFOST/CGMS for the albedo  for a bare soil, a canopy and a water surface a value of 0.15,  0.25 and 0.05 are assumed respectively.
 

Table 4.2. Albedo values for wet and dry soils (ten Berge, 1986)

 

Surface type	Wet	Dry
Dune sand	0.24	0.37
Sandy loam	0.10-0.19	0.17-0.23
Clay loam	0.10-0.14	0.20-0.23
Clay	0.08	0.14

The evaporative demand of the atmosphere depends on the difference between saturated and actual vapour pressure and on the wind function. For crop canopies the evaporative demand is somewhat higher than for soil or water surfaces due to a higher surface roughness. This is reflected in a higher value for f_c in the wind function.

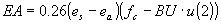(4.19)

where	EA	:	Evaporative demand	[mm d-1]
	es	:	Saturated vapour pressure (see eq.  4.9)	[hPa]
	ea	:	Actual vapour pressure	[hPa]
	fc	:	Empirical constant	[-]
	BU	:	Coefficient in wind function (see eq. 4.4)	[-]
	u(2)	:	Mean windspeed at 2 m height	[m s-1]

For crop canopies  f_c  = 1.0 and for a free water surface  f_c  = 0.5 are assumed (Frère, 1979). Substituting equation 4.15 in equation 4.1 yields

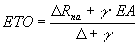(4.20)

where	ET0	:	Evapo(transpiration)	[mm d-1]
	Rna	:	Net absorbed radiation (see eq. 4.18)	[mm d-1]
	EA	:	Evaporative demand (see eq. 4.19)	[mm d-1]
	D	:	Slope of the saturation vapour pressure curve	[hPa °C-1]
	g	:	Psychrometric constant	[hPa °C-1]

Through introducing different values for albedo into equation (4.20), evapo(transpi)ration from a wet bare soil surface E0_s, a water surface, E0_w, and a crop canopy, ET0, can be calculated.
 
 

4.2. Day length and solar elevation

Subroutine Astro calculates day length, some intermediate variables for the calculation of the solar elevation, the integral of the solar elevation over a day and the fraction of diffuse radiation.

Day length is a function of the solar elevation (i.e. angle of the sun above the horizon) which is the angle between the sun rays and the earth's surface. Solar elevation is determined by latitude, the day and the hour on a certain day. The sine  of the solar elevation can be calculated as (Penning de Vries & van Laar, 1982):

(4.21)

where	b	:	Solar elevation	[radians]
	l	:	Latitude	[radians]
	d	:	Solar declination	[radians]
	th	:	Hour of the day (solar time)	[h]

To explain the dependency of solar elevation on latitude and day number first the situation is regarded when the sun is in zenith. This is at 12 o'clock solar time (not to be mixed up with noon). The solar declination, the place were the sun is in zenith at 12 o'clock solar time, changes every day. On the 21^st of June the sun stands perpendicular above the northern tropic of Cancer (+23.45°N) and on the 22^nd of December the sun stands perpendicular above the tropic of Capricorn (-23.45°S). In figure 4.1 the situation is depicted for 22^nd of December when the sun reaches its highest point at the tropic of Capricorn at the southern hemisphere. On the northern hemisphere this results in the shortest day of the year.

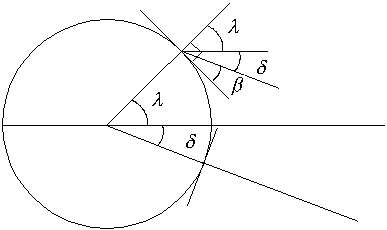
Figure 4.1. Solar declination

The solar declination during the year can be approached by a cosine function. (Note a shift of ten days).

(4.22)

where	d	:	Solar declination	[radians]
	td	:	Number of the day since 1 January	[-]

The distance of the sun to the earth is considered to be infinite, therefore declination can be considered equal for all places on earth. The orbit of the earth around the sun is a non concentric ellipse (see figure 4.2), therefore the solar radiation received at the top of the atmosphere during the year is not constant. At the first of January the earth is closest to the sun, radiation at the top of the atmosphere will then be higher as during other days.

Figure 4.2. Orbit of the earth around the sun

The average solar radiation at the top of the atmosphere is estimated at 1370 W m^-2. A daily solar radiation constant can than be calculated as a cosine times the average solar radiation at the top of the atmosphere multiplied by correction factor to correct for the elliptical orbit of the earth around the sun. This correction factor is estimated to be 0.033.

(4.23)

where	Sc,d	:	Solar constant at the top of the atmosphere for a certain day	[J m-2 s-1]
	Sc	:	Average solar radiation at the top of atmosphere	[J m-2 s-1]
			(1370 J m-2 s-1; I.e.A., 1978)
	td	:	Number of day since 1 January	[-]

Note that during the winter in Europe the solar radiation at the top of the atmosphere is at its maximum!

To compute day length for photoperiod-sensitive species, it must be realized that, even when the sun is still below the horizon the light level is high enough to trigger the photoperiodicity mechanism. Photoperiodic day length is 0.5 h longer than the astronomical day length at the equator and about 0.8 h in temperate zones, depending on the date of the year. The light level to which photoperiodism is sensitive is quite low and not well quantified. Vergara & Chang (1985) determined it to be 1.5-15 mW m^-2 for rice crops; Salisbury (1981) determined the level to be higher.  The photosynthetic active period and the astronomical day length can be calculated as:

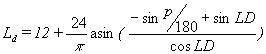(4.24)

where	Ld	:	Day length	[h]
	sinLD	:	Seasonal offset of sine of solar height = sindsinl	[-]
	cosLD	:	Amplitude of sine of solar height = cosdcosl	[-]
	p	:	correction constant	[degrees]

As a compromise for the photoperiodic day length a value of 50 mW m^-2, which corresponds with a sun angle of -4 degrees, can be applied in WOFOST.  For the astronomical day length the correction constant is -0.833 degrees (i.e. solar height for which the upper edge of the solar disk appears on the horizon). However, in WOFOST/CGMS for the calculation of the astronomical day length, a correction constant is set to 0 degrees.

The calculation of the photoperiodic day length makes no sense when the sun is continuously at higher inclinations, therefore this calculation method is limited to -66.5+4 and 66.5-4 degrees of latitude.

The integral of the solar height over the day can be obtained as twice the integral from sunrise (b=0°) to 12 o'clock solar time (b = 90° + d -l):

	(4.25)

where		:	Integral solar height	[s]
	D	:	Day length	[h]
	b	:	Solar elevation	[radians]
	th	:	Hour of the day	[h]

Multiplication of equation 4.22 with 4.24 yields the daily extra-terrestrial radiation (a.k.a. Angot radiation).

(4.26)

where	Ra,d	:	Daily extra-terrestrial radiation	[J m-2 d-1]
	Sc,d	:	Solar constant at the top of the atmosphere for a certain day (see eq. 4.23)	[J m-2 s-1]
	th	:	Hour of the day	[-]

In WOFOST/CGMS the integral of the effective solar height, a modification of equation 4.26 is also calculated. This modified integral takes the effect of the daily course in atmospheric transmission into account. Due to haze in the morning and clouds in the afternoon, transmission is lower near the margins of the day. Besides that, path length of solar radiation in the atmosphere is longer (Spitters et al., 1986). The modified integral can be calculated as:

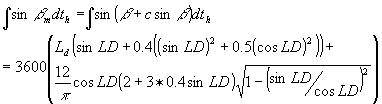(4.27)

where		:	Integral of effective solar height	[s]
	D	:	Day length	[h]
	c	:	Coefficient of regression on transmission on solar angle = 0.4	[-]
	b	:	Solar elevation	[radians]
	l	:	Latitude	[radians]
	d	:	Solar declination	[radians]
	th	:	Hour of the day	[h]

In WOFOST/CGMS diffuse sky light, with incidence under various angles, and direct sunlight, with an angle of incidence equal to the solar declination, are distinguished. This distinction accounts for the large difference in illumination intensity between shaded leaves and sunlit leaves and therefore the difference in the CO₂ assimilation light response of single leaves (which is non-linear). Shaded leaves receive only diffuse radiation. Sunlit leaves receive both direct and diffuse radiation. The diffuse flux is the result of the scattering of sun rays by clouds, aerosols and gases in the atmosphere. The proportion of diffuse light in the total incident light flux depends on the status of the atmosphere, i.e. cloudiness, concentration of aerosols. This fraction is calculated from the atmospheric transmission using an empirical function. This relationship is based on data from different meteorological stations from a wide range of latitudes and longitudes (Spitters et al., 1986).

The relation between the proportion of the diffuse flux in the global irradiance (R_df/R_g) and the atmospheric transmission T_atm (i.e. R_g/R_a) are found in several research reports concerning the use of solar energy in solar collectors. This relation is characterized by an approximately linear trend for transmissions ranging between 0.35 and 0.75. At low transmissions, nearly all of the incoming radiation is diffuse so that the curve bends off.

There is some variation among published relations, arising from differences in atmospheric conditions, especially reative sunshine duration, water content of the atmosphere, and cloud type, but also lack of fit of the presented regression equation from the data and differences in the method of measuring the diffuse radiation.

The relation used in WOFOST/CGMS has been derived by de Jong (1980) and has been recommended by Spitters et al. (1986).

	for  Tatm £0.07	(4.28a)
	0.07 < for  Tatm £0.35	(4.28b)
	0.35 < for  Tatm £0.75	(4.28c)
	for  Tatm > 0.75	(4.28d)

where	Rdf,d	:	Daily diffuse radiation	[J m-2 d-1]
	Rg,d	:	Daily global radiation	[J m-2 d-1]
	Ra,d	:	Daily extra-terrestrial radiation (see eq. 4.26)	[J m-2 d-1]

In  subroutine Radfract these equations are applied. The presented equations are remarkably constant over climates and latitudes and consequently valid for a wide range of conditions (Spitters et al., 1986).

Measured or estimated daily total solar irradiation (wavelength 300-3000 nm) is input for WOFOST/CGMS. Only half of this incoming radiation is photosynthetical active (PAR, Photosynthetical active radiation, wavelength 400 - 700 nm). The photosynthetical active diffuse radiation, perpendicular to the direction of the solar rays can be calculated as:

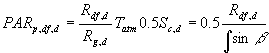(4.29)

where	PARp,df	:	Diffuse irradiation perpendicular to the direction of light	[J m-2 s-1]
	Tatm	:	Atmospheric transmission (i.e. Rg/Ra)	[-]
	Sc,d	:	Solar constant at the top of the atmosphere for a certain day	[J m-2 s-1]
	Rg,d	:	Daily global radiation	[J m-2 d-1]
	Rdf,d	:	Daily diffuse radiation (see eq. 4.28)	[J m-2 d-1]

The instantaneous incoming photosynthetically active radiation is calculated by multiplying half of the daily global radiation with the ratio of the actual effective solar elevation and the integral of the effective solar height:

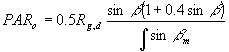(4.30)

where	PARo	:	Photosynthetically active radiation flux	[J m-2 s-1]
	Sg,d	:	Daily global radiation	[J m-2 d-1]
		:	The corrected integral of solar height over the day for non homogeneous atmospheric transmission (see eq. 4.27)	[s]

Photosynthetically active radiation flux consists of a diffuse flux and a direct flux. The diffuse flux is the result of scattering of sun rays by clouds, aerosols and gases in the atmosphere. The proportion of diffuse light in the total incident light flux depends on the status of the atmosphere. This fraction is calculated from the atmospheric transmission using an empirical function (Spitters et al., 1986).

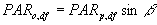(4.31)

where	PARo,df	:	Diffuse part of the photosynthetically active radiation flux at top of the canopy	[J m-2 s-1]
	PARp,df	:	Diffuse radiation perpendicular to the direction light	[J m-2 s-1]

The direct part can be easily obtained by subtracting the diffuse part from the photosynthetically radiation flux:

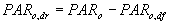(4.32)

where	PARo,dr	:	Direct part of the photosynthetically active radiation flux at top of the canopy	[J m-2 s-1]
	PARo	:	Photosynthetically active radiation flux	[J m-2 s-1]
	PARo,df	:	Diffuse part of the photosynthetically active radiation flux at top of the canopy	[J m-2 s-1]

4.3. Interpolation of daily meteorological data

The interpolation method implemented in WOFOFS/CGMS  follows the recommendations of the study carried out by SC-DLO by van der Voet et. al., (1994) and is described by van der Goot (1998).

Basis of the interpolation is selection of suitable meteorological stations for determination of representative meteorological conditions for a grid cell. The actual interpolation, once this selection has been made, is a simple average for most of the meteorological parameters, corrected for an altitude difference in case of temperature and vapour pressure. The exception is the rainfall data, which is taken directly from the most suitable station.
 

4.3.1. General selection of weather stations

Not all of the meteorological stations broadcast a complete set of data via the Global Telecommunication System (GTS), and not all of the stations are broadcasting all of the time. To increase the reliability of the interpolation, and to reduce the computational requirements a number of checks is performed on the availability of the data from the weather stations. The first check is based on a classification with respect to the type of data that the station can deliver. Three classes are being distinguished: rainfall data, temperature data and all other data. The second check is based on the temporal availability of the data in these classes. The selection procedure determines for each weather station if the availability for a class of data falls above a certain threshold. If so, then the station will be marked as a valid station for that type of data. The threshold value can be selected per station, but is applied to all three categories. A typical example would be a threshold value of 80%, i.e. if the station data in a particular class is available for more than 80% of the time, the station will be used for the interpolation of the data in that class. The timeframe taken into account for the check is the total number of days in the year for past years, and the number of days up to the . end-of-simulation. day in the current year.
 
 

4.3.2. Qualification of weather stations

To establish the suitability of a weather station for the interpolation, a selection procedure is applied that relies on the similarity of the station and the grid centre. This similarity is expressed as the result of a scoring algorithm that takes the following characteristics into account:

• Distance
• Difference in altitude
• Difference in distance to coast
• Climatic barrier separation

The final score is expressed in kilometres and is derived from these geographic characteristics by empirically converting them into kilometres. The higher the score, the less the similarity between the station and the grid centre. The score is calculated as follows:

Score = dist + Dalt*Walt + DdCstcorr + ClbInc

(4.33)

where	dist	:	Distance between the weather station and the grid centre	[km]
	Dalt	:	Absolute difference in altitude	[m]
	Walt	:	Weighting factor for Dalt (= 0.5)	[km/m]
	DdCstcorr	:	Absolute difference in corrected distance to coast (see below)	[km]
	ClbInc	:	Climate barrier increment.  (see below)	[km]

The climate barrier increment is set to 1000 when the station and the grid centre are separated by a climate barrier, otherwise it is set to 0.

The difference in the distance to the coast is expected to be more important when the absolute distance to coast is small, and of no importance when the actual distance to the coast is large. The empirical correction maps the true distance to coast to a range between 0 and 100 km.
 
 

4.3.3. Interpolation of rainfall data

In the current implementation of CGMS precipitation data is not interpolated. The precipitation for a grid is taken from the weather station that is the most similar (as explained above) to the grid centre, i.e. the station with the lowest score.
 
 

4.3.4. Interpolation of the other data

All other data is interpolated using data from up to four stations. To determine which stations to use, and indeed how many stations to use, a combination score is used. This combination score is calculated in a similar way to the single station score, but is based on the mean values of the combination of stations. The set score is calculated as follows:

SetScore = distavg + Daltavg*Walt + DdCstcorravg + DCG + FnS*Scoremin

(4.34)

where	distavg	:	Average distance between the stations and the grid centre	[km]
	Daltavg	:	Average of the absolute difference in altitude	[m]
	Walt	:	Weighting factor for Dalt (= 0.5)	[km/m]
	DdCstcorravg	:	Average of the absolute difference in corrected distance to coast	[km]
	DCG	:	Distance between the grid centre and the centre of gravity of the set of stations	[km]
	FnS	:	Factor based on the number of stations in the set (see below)	[-]
	Scoremin	:	Minimum single station score from the complete set of scores	[-]

The factor FnS increases as the number of stations in the set decreases. It is 0 for three or four stations in the set, 0.2 when two stations are used and 0.5 for a set consisting of a single station. The term FnS*Scoremin is used to balance the importance of the number of stations in relation to the other components.

Theoretically the set score could be calculated for all possible combinations of up to four stations, taken from all available stations. However it is clear that this would lead to many unnecessary calculations. Calculation of the set score is therefore only carried out for all combinations of up to 4 stations, taken from the seven stations most similar to the grid centre. This results in 98 sets for which the set score has to be calculated.

Once the best set of stations for the interpolation of the data for this grid has been established, as expressed by the minimum set score, the data is simply averaged. For the temperature and the vapour pressure, the result of the averaging is corrected for the difference in altitude between the centre of gravity of the set of selected stations, and the altitude of the grid centre. The correction factor used for the temperature is -0.006, and the correction factor used for the vapour pressure is -0.00025.
 
 

4.3.5. Missing data

As mentioned previously, an availability threshold is applied to the weather stations used for the interpolation of meteorological data. This implies that a station can be missing data for a number of days, and still be deemed suitable for interpolation. In this case, when data for a given day is not available, it is substituted with the long-term average for that station for that day. This long-term average is calculated using the complete set of historical data available for the station. The procedure to calculate this long-term average is as follows. First, for every Julian day, calculate the average value for all available meteorological parameters. Second, when for a given day an average value is not available, try to substitute this value by stepping back in time until a value is found, and use this for the current day. The stepping-back in time rolls over from Jan 1st to December 31st and is limited to 30 days. If no value is found, a long-term average for this day is not available.