5 CROP
5.1. Simulation of continuous processes
In WOFOST/CGMS plant and soil water subprocesses are separated into rate and state sections. Basic knowledge of the state variable approach, as it is used in continuous simulation, is assumed (see e.g. van Kraalingen, 1991; Penning de Vries & van Laar, 1982; de Wit & Goudriaan, 1978). To integrate processes over a certain time frame such as for example the growing period, the Euler integration method is used. For integration of individual processes over for example the canopy depth, or one day the Gaussian integration method is aplied. The state variables are calculated with the Euler integration method according to (van Kraalingen, 1991):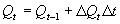 |
(5.1)
|
| where | Qt | : | State variable at time step t | [unit] |
| DQt | : | Rate variable at time step t | [unit d-1] | |
| Dt | : | Time step | [d] |
In theory, sequence in which various state variables are updated,
is not important because their values should not depend on each other but
should be fully determined by the rate variables. In practice however,
state variables may sometimes be derived from other state variables (e.g.
root/shoot ratio or total weight of leaves equals weight of dead leaves
plus weight of green leaves). It is therefore important to put state
and rate calculations in the right order and to ensure correct simulation
results are correct. If this rule is not applied, there is a risk that
some rates will pertain to states at current time step whereas others
will pertain to states from the previous time step.
5.2. Overview of the crop growth model
WOFOST/CGMS describes phenological development, growth and yield formation of a crop from emergence till maturity on the basis of crop genetic properties and environmental conditions. It simulates dry matter accumulation of a crop as a function of irradiation, temperature and crop characteristics in time steps of one day.Basis for calculating dry matter production, is the gross CO2 canopy assimilation rate, which depends on the absorbed radiation energy and is a function of incoming radiation and crop leaf area. From the absorbed radiation and the photosynthetic characteristics of single leaves, the daily CO2 crop assimilation rate is calculated. Part of the carbohydrates produced (CH2O) are used to provide energy for maintenance of existing live biomass (maintenance respiration). Remaining carbohydrates are converted into structural matter. During this proces some weight is lost due to growth respiration. Growth rate is obtained as:
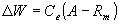 |
(5.2)
|
| where | DW | : | Growth rate | [kg Dry Matter ha-1 d-1] |
| A | : | Gross assimilation rate | [kg CH2O ha-1 d-1] | |
| Rm | : | Maintenance respiration rate | [kg CH2O ha-1 d-1] | |
| Ce | : | Conversion efficiency off assimilates, total crop | [kg Dry Matter kg-1 CH2O] |
Produced dry matter is partitioned amongst roots, leaves, stems and storage organs, using partitioning factors that are a function of the phenological development stage of the crop (Spitters et al., 1989). Fraction partioned to the leaves, determines leaf area development and hence dynamics of light interception. Dry weights of plant organs are obtained by integrating their growth rates over time (see eq. 5.1).
Leaf mass is subdivided into age classes. During crop development a part of living biomass dies due to senescence. Some simulated crop growth processes are influenced by temperature, like for example maximum photosynthesis and maintenance respiration rate. Other processes like partitioning of assimilates or decay of crop tissue are steered by the phenological stage. Phenological development stage is calculated as a function of ambient temperature and possibly modified the day length. An overview of all these processes is presented in Figure 5.1. (this figure is similar to Figure 2.6.)
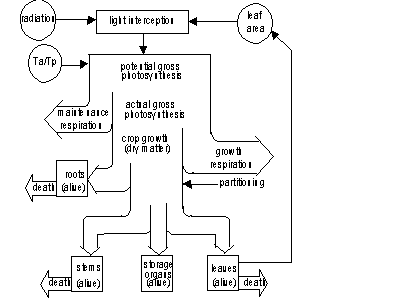
Figure 5.1. Overview of the crop growth processes. Ta and Tp are actual and potential transpiration rate. (de Koning et al., 1993)
Simulated processes include phenological development rate,
CO2 assimilation, maintenance respiration, dry matter partitioning
resulting in biomass accumulation, growth and senescence of leaves, transpiration
and extension of roots. Equations describing these processes
are treated in following sections.
5.3. Phenological development of a crop
Physiological plant age is defined by development stage, which is characterized by formation of various organs and their appearance. The most important phenological change is from vegetative to reproductive stage, which determines a large redirection of dry matter allocation over the plant organs. As many physiological and morphological processes change with phenological stage, its accurate quantification is essential in any crop growth simulation model. For many annual crops, development stage can conveniently be expressed in a dimensionless variable, having the value 0 at seedling emergence, 1 at flowering and 2 at maturity (van Heemst et al., 1986a; 1986b).5.3.1. Crop emergence
As start of the growing season sowing or emergence date can be selected, however if sowing date is selected, WOFOST/CGMS determines the emergence date and thus the start of the crop growth simulation. Crop emergence can be defined as a function of the effective daily temperature sum since sowing date. Emergence takes place when the effective daily temperature sum reaches the emergence threshold temperature. This threshold temperature is crop specific and should be given by the user. Daily effective temperature depends on the base temperature, below which no phenological processes take place, and the maximum daily temperature, beyond which phenological activity does not increase anymore. An example is depicted in Figure 5.2.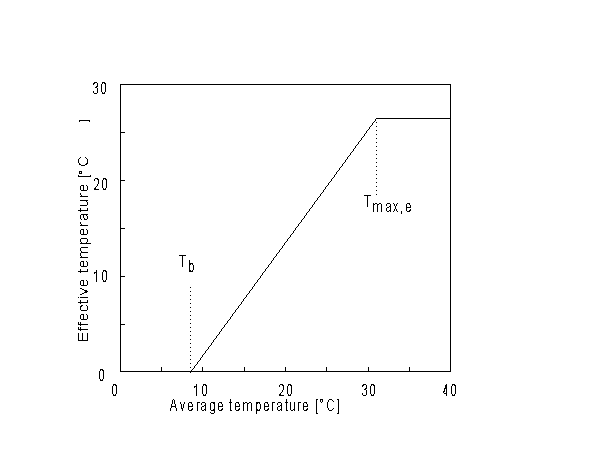
Figure 5.2. Effective temperature from sowing to emergence
The following relationship can be defined for the effective temperature sum:
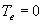 |
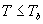 |
(5.3a)
|
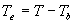 |
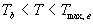 |
(5.3b)
|
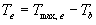 |
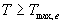 |
(5.3c)
|
| where | Te | : | Effective daily temperature | [°C] |
| Tmax,e | : | Maximum temperature beyond which phenological activity does not increase | [°C] | |
| Tb | : | Base temperature below which phenological development stops | [°C] | |
| T | : | (Average) daily temperature | [°C] |
Base temperature, Tb, is defined as the lower threshold temperature below which phenological activity stops. It is a crop specific and should be provided by the user. Maximum temperature beyond which phenological activity does not increase, Tmax,e is also crop specific and should be given by the user. Species originating from temperate regions show a base temperature of 0-3°C, while species of subtropical and tropical origins have a base temperature of 9-14°C (Angus et al., 1981). Within a species, cultivars may vary substantially in their temperature requirements. The temperature sum, therefore, must be characterized for each cultivar or group of cultivars (maturity classes).
Start of the growing season can be either sowing date or emergence day.
Sowing should be provided by the user or alternatively can be calculated by
the model (see Appendix IV).
5.3.2. Phenological development stage
A crop passes through successive phenological development stages, which length depends on the development rate. Development rates before and after anthesis are controlled by day length and/or temperature. In WOFOST/CGMS before anthesis both factors can be active, after anthesis only temperature influence is possible.Temperature is the main environmental factor affecting development
rate. Higher temperatures accelerate it, leading to shorter
growing periods. It responds to temperature according to a curvilinear
relationship. However, van Dobben, 1962 and van Keulen & Seligman, 1987
demonstrated, that over a wide range of temperatures, development rate
increases more or less linearly with temperature.
Development rate (for most crops) is expressed on a numerical scale
that ranges from 0 to 2, with 0 being emergence, 1 anthesis and 2 maturity.
It can be defined as that part of the scale that is accumulated
per day for a given variety. For example, if the time lapse between emergence
and anthesis is 50 days, average development rate during the pre-anthesis
phase is 1/50 or 0.02 d-1. Development stage can also be
related to the temperature sum, expressed in degree days, that is the sum
of daily temperatures over the period emergence-anthesis or anthesis-maturity.
Development rate is then the ratio of daily temperature and temperature sum
(van Heemst, 1986a; 1986b). This assumes a proportionality between temperature
and development rate. Its validity is limited, however.
In WOFOST/CGMS a more flexible relation is used to calculate the development rate. The effective increase in temperature sum depends on the daily temperature (Summerfield & Roberts, 1987). This relation is specified in an AFGEN table, which allows for non-linearity (lower and upper threshold values and optimum ranges). Average temperature is the independent variable in this table. Development rate can be obtained by:
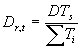 |
(5.4)
|
| where | Dr,t | : | Development rate at time step t | [d-1] |
| DTs | : | Temperature dependent correction factor | [°C] | |
| STi | : | Temperature sum required to complete stage i | [°C d] |
The temperature dependent correction factor, DTs and the temperature sum required to complete stage i, STi are crop dependent and should be provided by the user. Development stage at time step t is the integral of development rate over time (i.e. time span from emergence to current time step) and can be calculated according to:
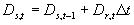 |
(5.5)
|
| where | Ds,t | : | Development stage at time step t | [-] |
| Dr,t | : | Development rate at time step t | [d-1] | |
| Dt | : | Time step | [d] |
For certain species or cultivars, during the vegetative stage (i.e. Ds < 1), day length effects should be taken into account. Approaches that describe such effects quantitatively are given amongst others by Weir et al. (1984), Hadley et al. (1984) and Reinink et al. (1986). In WOFOST/CGMS, a reduction factor for development rate as a function of day length is introduced. In case of photosensitivity, this reduction factor should be multiplied with equation (5.3). It can be calculated as:
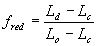 |
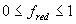 |
(5.6)
|
| where | fred | : | Development rate reduction factor as function of day length | [-] |
| Ld | : | Present day length (see eq. 4.24) | [h] | |
| Lc | : | Critical day length for development (lower threshold) | [h] | |
| Lo | : | Optimum day length for development (upper threshold) | [h] |
The user should provide information whether development rate depends
on temperature, on day length or both factors. Critical daylength, Lc
and optimum daylength, Lo are crop dependent and should
also be provided. Note that in modern cultivars, photosensitivity
is much less pronounced than in traditional cultivars, and for modelling
purposses day length influence can be ignored by choosing an
appropriate temperature sum, which lead to an equivalent crop life cycle.
Crop growth simulation stops when development stage reaches the
stage at which the crop will be harvested. This development stage should
be provided by the user.
5.4. Daily assimilation
Daily gross CO2 assimalation is the most detailed part of WOFOST/CGMS and a two step procedure is applied to describe this process. Each step will be described separately (Subroutine CSimCro):- Total daily gross CO2 assimilation rate of the canopy [Subsection 5.4.1.]
- Total instantaneous gross CO2 assimilation of the canopy [Subsection 5.4.2.]
5.4.1. Total daily gross CO2 assimilation rate of the canopy
To calculate the total daily gross CO2 assimilation rate for the whole canopy, an integration over the day should be executed. Therefore, for given photosynthetically active radiation fluxes, at three different periods of the day, total instantaneous gross canopy CO2 assimilation rate is computed. Subsequently, the integral (over time) is calculated as a weighted average of the three selected hours. To calculate the total instantaneous gross canopy CO2 assimilation rate, the gross instantaneous assimilation rate should be integrated over the canopy depth. Therefore, at three different dephts in the canopy gross instantaneous assimilation rate is calculated and subsequently the integral (over depth), as a weighted average of selected depths, is computedDaily total assimilation calculation, is only necessary if instantaneous assimilation takes place. It will be zero if leaf area index equals zero (no photosynthetic activity) or when the maximum CO2 assimilation rate at light saturation equals zero. Maximum CO2 assimilation rate is a function of development stage and is crop dependent.
As is mentioned before, to integrate the gross instantaneous assimilation rate over the day, three points in time are selected at which the photosynthetically active radiation is calculated. It is assumed that radiation is homogeneously distributed over the day according to the sine of the solar elevation. The weighted average CO2 assimilation rate can therefore be calculated for half a day only. The three points in time are selected from noon to sunset (this explains the use of the constants 0.5 and 12.00):
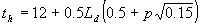 |
(5.7)
|
| where | Ld | : | Day length (see eq. 4.24) | [h] |
| th | : | Hour of the day | [h] | |
| p | : | Gaussian integration points | [-] |
These three values for th are introduced in equation
(4.21) and subsequently the results are used to calculate PARo,
PARo,df and PARo,dr, respectively. See equations
(4.30),
(4.31) and (4.32).
Once the photosynthetically active radiation fluxes have been established,
for each value of th, the canopy instantaneous gross assimilation
rate can be calculated (i.e. integration over the canopy depth, see next
section). Subsequently daily gross CO2 assimilation rate can be
established as the weighted average of the three selected
hours of the day (i.e. integration over time).
Multiplying by day length results in the total daily
gross rate of CO2 assimilation.
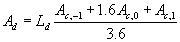 |
(5.8)
|
| where | Ad | : | Total gross assimilation rate | [kg ha-1 d-1] |
| Ld | : | Day length (see eq. 4.24) | [h] | |
| Ac | : | Total inst. gross assimilation rate for the whole canopy, p= -1,0,1 (see eq. 5.27) | [kg ha-1 h-1] |
5.4.2. Total instantaneous gross CO2 assimilation of the canopy
Reflection and extinctionPart of the total incoming photosynthetically active radiation flux is reflected by the canopy. The reflection coefficient is defined as fraction of the downward radiation flux that is reflected by the whole canopy. According to Goudriaan (1977), the reflection coefficient of a green leaf canopy with a random spherical leaf angle equals:
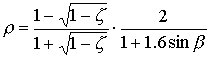 |
(5.9)
|
| where | r | : | Reflection coefficient of a green leaf canopy | [-] |
| z | : | Scattering coefficient fraction (transmission and reflection) of single
leaves
for visible radiation (=0.2; Goudriaan, cited by Spitters, 1986) |
[-] | |
| sin b | : | Sine of solar elevation | [-] |
The first term denotes the canopy reflection of horizontal leaves and the second term is the approximate correction factor for a spherical leaf angle distribution. A fraction (1-r) of incoming visible radiation is potentially available for absorption. Radiation fluxes attenuate exponentially within a canopy with increasing leaf area from the top downwards:
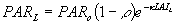 |
(5.10)
|
| where | PARL | : | Net photosynthetic active radiation flux at depth L in the canopy | [J m-2 s-1] |
| PARo | : | Photosynthetically active radiation flux (see eq. 4.30) | [J m-2 s-1] | |
| LAIL | : | Cumulative leaf area index (from top downwards) at relative depth L | [ha ha-1] | |
| r | : | Reflection coefficient of the canopy | [-] | |
| k | : | Extinction coefficient for photosynthetic active radiation flux | [-] |
Diffuse and direct radiation fluxes have different extinction coefficients, resulting in different light profiles within the canopy. Therefore three different radiation fluxes are distinguished:
- diffuse flux, with extinction coefficient kdf;
- total direct flux, with extinction coefficient kdr,t;
- direct component of direct flux, with extinction coefficient kdr,bl.
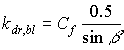 |
(5.11)
|
| where | kdr,bl | : | Extinction coefficient for the direct component of the direct flux | [-] |
For a spherical leaf area distribution (homogeneous, random), the extinction coefficient for the diffuse radiation flux equals:
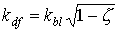 |
(5.12)
|
| where | kdf | : | Extinction coefficient for the diffuse radiation flux | [-] |
| kbl | : | Extinction coefficient for the direct radiation flux | [-] | |
| z | : | Scattering coefficient fraction of single leaves for visible radiation | [-] |
In WOFOST/CGMS, the diffuse radiation flux extinction coefficient, kdf is not computed but should be provided by the user. It can be measured directly under diffuse sky conditions. In equation 5.11, 0.5 indicates average projection on the ground surface of leaves that show a spherical angle distribution. Average extinction coefficient for the diffuse radiation flux is about 0.72 (Goudriaan, 1977). However, in many situations, leaf angle distribution is not spherical. In rice for example, leaves are clustered and have a very vertical orientation. Other leaf angle distributions can be accounted for by a procedure described by Goudriaan (1986), which calculates the extinction coefficient for diffuse radiation flux based on the frequency distribution of leaves with angles in different classes. In WOFOST/CGMS however, leaf angle distribution is accounted for by using a so called cluster factor which is the measured extinction coefficient for diffuse radiation flux, relative to the theoretical one, assuming a spherical leaf area distribution:
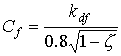 |
(5.13)
|
| where | Cf | : | Cluster factor | [-] |
| kdf | : | Extinction coefficient for diffuse radiation flux | [-] | |
| z | : | Scattering coefficient fraction of single leaves for visible radiation | [-] |
0.8 in equation 5.13 is the value of 0.5/sinb averaged over elevation b of incident radiation under an overcast sky. The extinction coefficient of the direct component can be calculated as (Goudriaan, 1977):
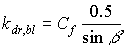 |
(5.14)
|
| where | kdr,bl | : | Extinction coefficient for the direct component of the direct radiation flux | [-] |
| Cf | : | Cluster factor | [-] |
The extinction coefficient for the total direct radiation flux can be calculated as (Goudriaan, 1977):
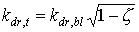 |
(5.15)
|
| where | kdr,t | : | Extinction coefficient for total direct radiation flux | [-] |
| kdr,bl | : | Extinction coefficient for the direct component of direct light | [-] | |
| z | : | Scattering coefficient | [-] |
Absorption
Three depths in the canopy are selected according to the Gaussian integration method and at those levels leaf area index, amount of absorbed radiation and leaf CO2 assimilation are calculated. Total instantaneous assimilation is easily obtained by multiplying instantaneous assimilation with the total leaf area index (eq. 5.27). In the following text calculation of the instantaneous assimilation will be explained in detail. Calculation of leaf area index will be explained in Subsection 5.5.5.. Canopy assimilation is calculated as a weighted average of the assimilation at three horizons. Leaf area index of these horizons can be calculated as (Goudriaan, 1986):
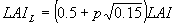 |
p= -1, 0, 1 | (5.16)
|
| where | LAIL | : | Leaf area index at relative distance L in the canopy | [ha ha-1] |
| (L=0 at the top) |
Light absorbed at a certain depth in the canopy is obtained by taking the derivative of equation (5.10) with respect to the cumulative leaf area index:
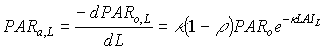 |
(5.17)
|
| where | PARa,L | : | Amount absorbed of total radiation flux at relative depth L | [J m-2 s-1] |
| PARo,L | : | Net photosynthetic active radiation at relative depth L in the canopy | [J m-2 s-1] | |
| PARo | : | Photosynthetically active radiation flux at top of the canopy | [J m-2 s-1] | |
| L | : | Relative depth in the canopy | [-] | |
| k | : | The extinction coefficient for the PAR flux | [-] | |
| r | : | Reflection coefficient of the canopy (see eq. 5.9) | [-] |
Absorbed fluxes for the different light components per unit leaf area at a certain canopy depth can be expressed as:
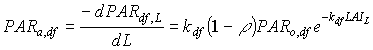 |
(5.18a)
|
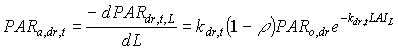 |
(5.18b)
|
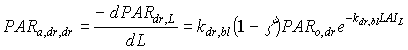 |
(5.18c)
|
| where | PARa,. | : | Amount absorbed of specified radiation flux | [J m-2 s-1] |
| PAR.,L | : | Net specified component of PAR flux at relative depth L | [J m-2 s-1] | |
| PARo | : | Photosynthetically active radiation flux at top of the canopy | [J m-2 s-1] | |
| L | : | Relative depth in the canopy | [-] | |
| k. | : | The extinction coefficient for specified radiation (see eq. 5.12, 5.14 and 5.15) | [-] | |
| r | : | Reflection coefficient of the canopy (see eq. 5.9) | [-] | |
| z | : | Scattering coefficient | [-] | |
| bl | : | Black | ||
| df | : | Diffuse | ||
| dr | : | Direct | ||
| t | : | Total |
Note that of the direct component of the direct flux the non-scattered part (1-z) is absorbed. The total absorbed flux for shaded leaves can be calculated as the sum of the absorbed flux of diffuse radiation and absorbed flux of the diffuse radiation of the indirect component of direct radiation, which equals the difference of the absorbed flux of total radiation minus the absorbed flux of the direct component of the direct radiation:
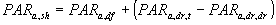 |
(5.19)
|
| where | PARa,sh | : | Absorbed amount of the total radiation flux by shaded leaves | [J m-2 s-1] |
| PARa,df | : | Absorbed amount of the diffuse radiation flux | [J m-2 s-1] | |
| PARa,dr,t | : | Absorbed amount of the total direct radiation flux | [J m-2 s-1] | |
| PARa,dr,dr | : | Absorbed amount of direct component of the direct radiation flux | [J m-2 s-1] |
Instantaneous gross assimilation
The absorbed amount of radiation is introduced into an assimilation-light response function to obtain the CO2 assimilation-light response for individual leaves. Satisfactory results can be acquired with (Peat, 1970):
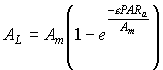
| (5.20)
|
| where | AL | : | Inst. gross assimilation rate at relative depth L (per unit leaf area) | [kg ha-1 h-1] |
| Am | : | Inst. gross assimilation rate at light saturation | [kg ha-1 h-1] | |
| e | : | Initial light use efficiency | (kg ha-1 h-1)/(J m-2 s-1) | |
| PARa | : | Absorbed amount of the total radiation flux | [J m-2 s-1] |
The instantaneous gross assimilation rate at light saturation, Am, is crop specific and a function of development stage, it should be provided by the user. An AFGEN table with development stage as independent variable is used to describe this dependency. Initial light use efficiency, e, is also crop dependent and should be provided by the user. It is assumed, that the initial light use efficiency is always higher than 2.0 [kg ha-1 leaf h-1]. Introducing the absorbed radiation amount by shaded leaves (eq. 5.19) into equation 5.20 yields:
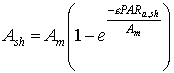
| (5.21)
|
| where | Ash | : | Inst. gross assimilation rate for shaded leaves | [kg ha-1 h-1] |
| Am | : | Inst. gross assimilation rate at light saturation | [kg ha-1 h-1] | |
| e | : | Initial light use efficiency | (kg ha-1 h-1)/(J m-2 s-1) | |
| PARa,sh | : | Absorbed amount of the total radiation flux by shaded leaves (see eq. 5.19) | [J m-2 s-1] |
For the sunlit leaf area, average absorption intensity may be substituted in equation 5.20. However, it is more accurate to account for variation in leaf angle and thus in illumination intensity (Spitters, 1986). The direct flux is absorbed by a leaf perpendicular to the direct beam with an intensity of:
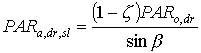 |
(5.22)
|
| where | PARa,dr,sl | : | Absorbed amount of the direct radiation flux by leaves perpendicular to the direct beam | [J m-2 s-1] |
| PARo,dr | : | Direct flux of visible radiation at the top of the canopy | [J m-2 s-1] | |
| z | : | Scattering coefficient | [-] | |
| sin b | : | Sine of solar elevation | [-] |
The amount of absorbed direct radiation (eq. 5.22) depends on the sine of incidence at the leaf surfaces. Therefore, for leaves with different angles CO2 assimilation rates have to be calculated separately and integrated over the sine of incidence. However, in WOFOST/CGMS a spherical leaf angle distribution is assumed, consequently no integration over leaf angles is needed. Integration over the sine of incidence for sunlit leaves yields (Goudriaan, personal communication):
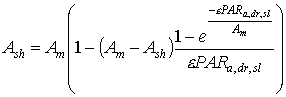 |
(5.23)
|
| where | Asl | : | Inst. gross assimilation rate for sunlit leaves | [kg ha-1 h-1] |
| Ash | : | Inst. gross assimilation rate for shaded leaves | [kg ha-1 h-1] | |
| Am | : | Inst. gross assimilation rate at light saturation | [kg ha-1 h-1] | |
| PARa,dr,sl | : | Absorbed amount of the direct radiation flux by leaves perpendicular to the direct beam | [J m-2 s-1] | |
| e | : | Initial light use efficiency | (kg ha-1 h-1)/(J m-2 s-1) |
The assimilation rate per unit leaf area at a specific canopy depth is the sum of assimilation rates of sunlit and shaded leaves, taking the proportion of sunlit and shaded leaf area at that canopy depth into account. The fraction sunlit leaf area equals the fraction of direct radiation reaching that layer:
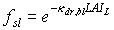 |
(5.24)
|
| where | fsl | : | Fraction sunlit leaf area | [-] |
| kdr,bl | : | Extinction coefficient for the direct component of direct radiation (see eq. 5.14) | [-] | |
| LAIL | : | Cumulative leaf area index at relative depth L in the canopy | [-] |
The total instantaneous assimilation rate at a relative depth L can be calculated as:
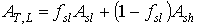 |
(5.25)
|
| where | AT,L | : | Total inst. gross assimilation rate at a relative depth L | [kg ha-1 h-1] |
| Asl | : | Inst. gross assimilation rate for sunlit leaves | [kg ha-1 h-1] | |
| Ash | : | Inst. gross assimilation rate for shaded leaves | [kg ha-1 h-1] | |
| fsl | : | Fraction sunlit leaf area | [-] |
Total instantaneous canopy assimilation rate per unit leaf area is established using the Gaussian integration method, as a weighted average of the assimilation at three levels within the canopy.
- first the leaf area index for the three selected horizons has to be established (see eq. 5.16)
- next these LAI values are introduced in the equations and the weighted average is calculated, which corresponds to the total instantaneous canopy assimilation rate.
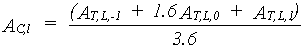 |
(5.26)
|
| where | AC,l | : | Total instantaneous canopy assimilation rate (per unit leaf area) | [kg ha-1 h-1] |
| AT,L,p | : | Total instantaneous gross assimilation rate at relative depth L at p= -1,0,1 (see eq. 5.25) |
[kg ha-1 h-1] |
Total instantaneous assimilation rate is calculated per unit leaf area and must therefore be multiplied with leaf area index to yield the total canopy assimilation rate:
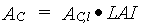 |
(5.27)
|
| where | AC | : | Total inst. gross assimilation rate for the whole canopy | [kg ha-1 h-1] |
| AC,l | : | Total inst. gross canopy assimilation rate per unit leaf area | [kg ha-1 h-1] | |
| LAI | : | Total crop leaf area index (see Subsection 5.5.5.) | [ha ha-1] |
Note that the green parts of stems and storage organs (like panicles)
may absorb a substantial amount of radiation. Therefore, the green area
index (of these) organs is added to the total leaf area. Green area index
of stems and storage organs can be calculated by multiplying the organ
dry weight with respectively the specific stem area and specific pod area
(see also Subsection 5.5.5. and eq.
5.49). Specific stem area and specific pod
area are crop specific and should be provided by the user.
5.5. Crop growth
Gross CO2 assimilation as discussed in chapter 5.4 is the basis for crop growth. The resulting actual crop growth depends further on a number of assimilation reducing factors and assimilation requirements for maintenance respiration and bio-synthesis (i.e. the conversion of primary assimilates into plant tissue). The remaining dry matter is partioned over various organs. Besides growth, plant organs organs also die. All these processes are simulated and described in the following sections.5.5.1. Actual gross photosynthesis
In Section 5.4, assimilation was treated as a function of intercepted radiation and of photosynthetic crop characteristics such as initial light use efficiency and maximum leaf CO2 assimilation at light saturation. The value of some crop characteristics are dependent on phenological crop stage. In addition, the assimilation process can be hampered by suboptimum temperatures and/or by reduced availability of CO2 due to closure of the leaf stomata as means to reduce transpiration. Thus, the gross assimilation depends on development stage, on temperature and on the transpiration rate. In this paragraph this dependency will be briefly explained.Development stage
As mentioned before, the instantaneous gross assimilation rate at light saturation, also called the maximum leaf CO2 assimilation rate, Am, is a function of development stage and is crop specific. An AFGEN table with the development stage as the independent variable is used to describe this dependency (see also Subsection 5.3.2.). For an example see Figure 5.3.
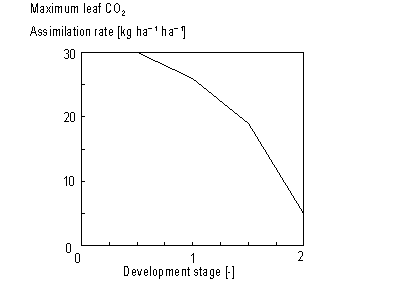
Figure 5.3. Maximum leaf CO2 assimilation
rate as a function of development stage.
Daytime temperature
Maximum leaf CO2 assimilation rate, Am, has to be corrected for sub-optimal average daytime temperatures. The correction factor is determined by daytime temperature and is crop specific. An AFGEN table with average day time temperature as independent variable is used to describe this dependency. For an example see Figure 5.4. The correction factor has to be multiplied with Am. The daytime temperature can be calculated as:
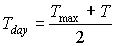 |
where | 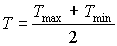 |
(5.27)
|
| where | Tday | : | Average daytime temperature | [°C] |
| T | : | (Average) daily temperature | [°C] | |
| Tmax | : | Maximum daily temperature | [°C] | |
| Tmin | : | Minimum daily temperature | [°C] |
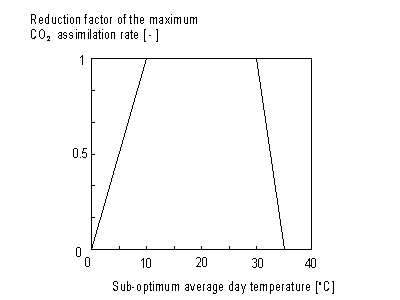
Figure 5.4. Reduction factor of maximum leaf CO2
assimilation as a function of average temperature.
Nighttime temperature
Gross CO2 assimilation rate cannot exceed the maximum CO2 assimilation rate. It should also be noted that assimilation is an enzymatic process and thus temperature dependent (Downes, 1970). However, there seems to be a considerable adaption of the assimilation processes to fluctuating and varying temperatures (de Wit et al., 1978). A wide temperature range for optimum photosynthetic performance under field conditions is observed (Wardlaw, 1974). Low nighttime temperatures also affect assimilation. At night assimilates, produced during daytime, are transformed into structural biomass. This process is hampered by low temperature. If these low temperatures prevail for a several days, assimilates accumulate in the plant and the assimilation rate diminishes and ultimately halts. In WOFOST/CGMS, this temperature effect is accounted for by introducing a correction factor, which should be multiplied with Am. This correction factor is a function of low minimum temperature and is crop specific. An AFGEN table is used to describe this dependency. As a measure for quantifying the low minimum temperature effect, the seven day running average of minimum temperature is used as independent variable in an AFGEN table.
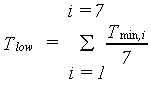 |
(5.29)
|
| where | Tmin | : | Daily minimum temperature | [°C] |
| Tlow | : | Seven day running average of minimum temperature | [°C] | |
| i | : | Day | [-] |
Photosynthesis in terms of CH2O
In the photosynthesis process, CO2 is reduced to carbohydrates (CH2O) using the energy supplied by the absorbed light. The overall chemical reaction of this complex process is:
 |
(5.30)
|
 |
(5.31)
|
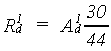 |
(5.32)
|
| where | R1d | : | Gross daily CH2O assimilation rate | [kg ha-1 d-1] |
| (not corrected for water stress) | ||||
| A1d | : | Gross daily CO2 assimilation rate (see eq. 5.8) | [kg ha-1 d-1] | |
| (corrected for low minimum temperature) |
As mentioned earlier, the gross daily CO2 assimilation rate,
A1d, can be calculated by multiplying the total instantaneous
assimilation rate (eq. 5.27) with day length
(eq. 4.24).
The calculated daily assimilation in CH2O per ha will be reduced when water stress occurs. In the model effects of water stress on assimilation are related to the ratio of actual transpiration and potential transpiration (van Keulen & Seligman, 1987). Gross assimilation rate, corrected for water stress, can be calculated as:
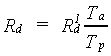 |
(5.33)
|
| where | Rd | : | Gross daily CH2O assimilation rate | [kg ha-1 d-1] |
| R1d | : | Gross daily CH2O assimilation rate (not corrected for water stress) | [kg ha-1 d-1] | |
| Ta | : | Actual transpiration | [cm d-1] | |
| Tp | : | Potential transpiration | [cm d-1] |
In §6.1 the calculation of potential, Tp, and actual
transpiration, Ta, will be explained.
5.5.2. Maintenance respiration
Some of the produced carbohydrates are respired to provide energy for maintaining existing biostructures. Maintenance includes resynthesis of degraded proteins (especially enzymes) and maintenance of ionic gradients across cell membranes. The higher the plant metabolic activity, the higher the maintenance costs (Penning de Vries, 1975), probably due to a higher enzyme turnover and higher transport costs. Maintenance respiration provides energy for living organisms to maintain their biochemical and physiological status. Through the reverse reaction of CO2 reduction in the CO2 assimilation, the fixed radiation energy is released in a suitable form (ATP and NADPH):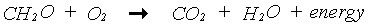 |
(5.34)
|
Maintenance respiration consumes roughly 15 - 30% of the carbohydrates
produced by a crop in a growing season (Penning de Vries et al.,
1979). This indicates the importance of accurate quantification of this
process.
Maintenance respiration as a function of the weight of dry matter
Maintenance costs may be estimated based on the (i)quantities of proteins and minerals present in the biomass and (ii) on crop metabolic activity, as presented by de Wit et al. (1978). This method, however, requires information on the nitrogen and mineral contents of the vegetation. Based on this analysis, typical values for the maintenance coefficients for various plant organs have been derived by Penning de Vries & van Laar (1982). In WOFOST/CGMS, these coefficients are used to calculate the crop maintenance requirements, which are approximately proportional to the dry weights of the plant organs to be maintained:
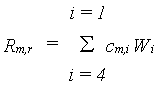 |
(5.35)
|
| where | Rm,r | : | Maintenance respiration rate at reference temperature of 25 °C | [kg ha-1 d-1] |
| cm,i | : | Maintenance coefficient of organ i | [kg kg-1 d-1] | |
| Wi | : | Dry matter weight organ i (see eq. 5.44) | [kg ha-1] | |
| i | : | Leaves (lv), storage organs (so), stems (st) or roots (rt) |
The maintenance coefficient of organ i, cm,i, is crop
dependent and should be provided by the user.
In Subsection 5.5.4., DWi, increase
of organ dry matter weight per time step, will be discussed. Integration of
DWi over previous time steps yields
the total organ dry matter weight (dead and alive). Integration of the
net increase of dry matter, DWni,
(see eq. 5.43) over previous time steps yields the living dry matter
weight of organ i (see eq. 5.44). Note that differences in nitrogen contents
in the different organs cause differences in the maintenance coefficients.
However, in the model nitrogen contents are not simulated.
Dependency of the maintenance respiration on development stage
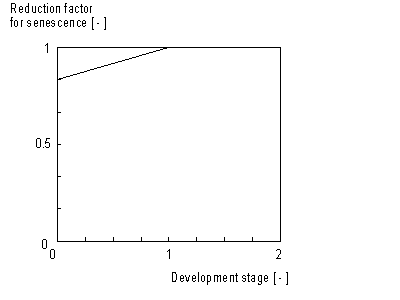
The calculated maintenance respiration rate (eq. 5.35) has to be corrected for senescence. This correction factor is crop specific and is defined as a function of development stage (see Figure 5.5.). An AFGEN table with development stage as independent variable, is used to describe this dependency. The maintenance respiration should be multiplied with this factor
Dependency of maintenance respiration on temperature
Higher temperatures accelerate turnover rates in plant tissue and hence costs of maintenance. An increase in temperature of 10°C increases maintenance respiration by a factor of about 2 (Kase & Catsky, 1984; Penning de Vries & van Laar, 1982). However, to be more flexible, a variable Q10 is introduced, which is defined as the relative increase of the respiration rate per 10°C temperature increase. Q10 should be provided by the user. Maintenance respiration rate at a certain temperature, can be calculated with:
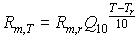 |
(5.36)
|
| where | Rm,T | : | Maintenance respiration rate at temperature T | [kg ha-1 d-1] |
| Rm,r | : | Maintenance respiration rate at reference temperature of 25 °C (see eq. 5.35) | [kg ha-1 d-1] | |
| Q10 | : | Relative increase of the respiration rate per 10°C temperature increase | [-] | |
| T | : | Average daily temperature | [°C] | |
| Tr | : | Reference temperature [=25 °C in the model] | [°C] |
For tropical species, the reference temperature may be 10°C higher than for species from temperate climates. The maintenance requirements of a crop are likely to be adapted to the higher growth temperatures. However, in WOFOST/CGMS the reference temperature is fixed at 25°C for all crops. As stated before, maintenance respiration rate depends on:
- the dry matter amount in various organs
- the relative maintenance rate per organ
- the temperature
5.5.3. Growth respiration
The primary assimilates in excess of the maintenance costs, are for conversion into structural plant material. In the conversion process of glucose molecules, CO2 and H2O are released. This is a partial combustion of glucose to provide energy required in various biochemical pathways. Hence, biosynthesis of various structural compounds can be considered a process of cut and paste, the scraps representing the weight lost in growth respiration. Each structural compound is formed along a distinct, non crop-specific pathway. Following these reactions, weight of glucose required to produce a unit of compound can be calculated (Penning de Vries et al., 1974). Transport costs of molecules are included. Two active passages of membranes are assumed. Each active passage requires 1 ATP, which is provided by respiring 1/38 molecule of glucose.The assimilates required to produce a unit weight of a certain plant organ can now be calculated from its chemical composition and the assimilate requirements of various chemical compounds. Storage organs (grains, tubers, etc.) vary too much in composition among species to provide one general value for their assimilate requirements. The conversion efficiency represents the inverse of the assimilate requirement. At higher temperatures the conversion processes are accelerated, but the pathways are identical (Spitters et al. 1989). Hence, the assimilate requirements do not vary with temperature. Growth respiration rate can be calculated as:
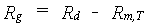 |
(5.37)
|
| where | Rg | : | Growth respiration rate | [kg ha-1 d-1] |
| Rd | : | Actual daily CH2O assimilation rate (see eq. 5.33) | [kg ha-1 d-1] | |
| Rm,T | : | Maintenance respiration rate at temperature T (see eq. 5.36) | [kg ha-1 d-1] |
5.5.4. Dry matter partitioning
As explained, conversion into dry matter costs energy, therefore a conversion factor is defined, which depends on the conversion efficiency of assimilates and on the partitioning factors of various plant organs. The dry matter is multiplied with this overall conversion efficiency factor to calculate the dry matter increase. The conversion efficiency of carbohydrates into structural plant material is calculated as a weighted average of the efficiencies for the various plant organs.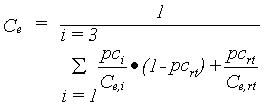 |
(5.38)
|
| where | Ce | : | Conversion efficiency factor of assimilates, total crop | [kg kg-1] |
| Ce,i | : | Conversion efficiency factor of the assimilates of a specified organ | [kg kg-1] | |
| pci | : | Partitioning factor of organ i | [kg kg-1] | |
| i | : | Leaves (lv), storage organs (so), stems (st) | ||
| rt | : | roots |
The conversion efficiency factor for the assimilates of a specified organ, Ce,i, is crop specific and should be given by the user. Total crop dry matter growth rate can be calculated as:
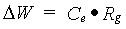 |
(5.39)
|
| where | DW | : | Dry matter growth rate total crop | [kg ha-1 d-1] |
| Ce | : | Conversion efficiency factor of assimilates, total crop (see eq. 5.38) | [kg kg-1] | |
| Rg | : | Growth respiration rate (see eq. 5.37) | [kg ha-1 d-1] |
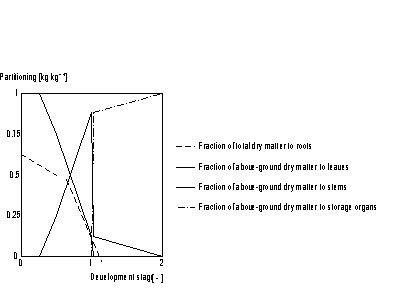
The pattern of dry matter distribution over various plant organs is closely related to crop development stage. Development is defined as progression in successive phenological stages. It is characterized by the formation rate of various vegetative and reproductive organs and their order of appearance. The remaining amount of absorbed CH2O after correction and reduction of the gross CO2 assimilation rate is the so called dry matter. Growth, in fact is the increase in biomass ignoring its water content. Dry matter is partitioned over roots, stems, leaves and storage organs. In WOFOST/CGMS, total dry matter growth is partitioned according to fixed distribution factors, defined as a function of development stage. Dry matter is first partitioned between shoots and roots.
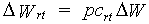 |
(5.40a)
|
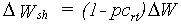 |
(5.40b)
|
| where | DW | : | Dry matter growth rate total crop | [kg ha-1 d-1] |
| DWrt | : | Dry matter growth rate roots | [kg ha-1 d-1] | |
| DWsh | : | Dry matter growth rate shoots | [kg ha-1 d-1] | |
| pcrt | : | Partitioning factor of roots | [kg kg-1] |
Growth rate of leaves, stems and storage organs is simply the product of the shoots dry matter growth rate and the fraction allocated to these organs.
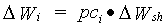 |
(5.41)
|
| where | DWi | : | Dry matter growth rate of organ i | [kg ha-1 d-1] |
| DWsh | : | Dry matter growth rate of shoots | [kg ha-1 d-1] | |
| pci | : | Partitioning factor of organ i | [kg kg-1] | |
| i | : | Leaves (lv), storage organs (so), stems (st) |
The partitioning factors, pci, are a function of development stage and are crop specific. The dependency is described using AFGEN tables with development stage as independent variable. At any development stage the following relation must be valid, if not, the simulation will be stopped (see also Figure 5.6.):
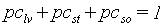 |
(5.42)
|
| where | pci | : | Partitioning factor of organ i | [kg kg-1] |
| i | : | Leaves (lv), storage organs(so), stems (st) |
Actual gross CO2 assimilation rate has to be identical to
the amount of structural plant material produced plus the amounts used
for maintenance respiration and conversion. Furthermore, it is assumed
that maintenance respiration can not exceed the actual gross assimilation
rate. However, when the daily CH2O assimilation rate comes close
to zero, this may happen and therefore simulation should be stopped.
5.5.5. Growth and leaf senescence
As is explained in Subsection 5.5.4., plant organ growth rate is obtained by multiplying the growth rate of that particular organ by the fraction of assimaltes allocated to it. Its total dry biomass (dead and alive) is obtained by integrating this growth rate over time. Taking death rate of various organs into account, integration of the net increase of dry matter, DWni, (see eq. 5.43) over the previous time steps yields the living dry matter weight of organ i (see eq. 5.44).This dry matter partitioning approach is descriptive, as the distribution
keys are defined as a function of crop development stage only. Influence
of environmental factors could be included by applying modification factors
to these keys, depending on temperature, water and nutrient status of the
crop, and its reserve level (Loomis et al., 1979; van Keulen &
Seligman, 1987). In WOFOST/CGMS, however, this is not applied. More attention
is paid to crop growth by introducing a death rate for leaves, roots and
stems. Death rate is a function of development stage and is crop and organ
specific.
Growth and growth rate
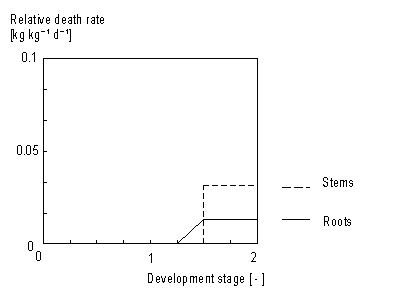
In WOFOST/CGMS storage organ death rate is considered to be zero. For roots and stems increase in living biomass can be easily determined as growth rate minus death rate. This yields the net growth rate (see eq. 5.43). Death rate is crop specific and is defined as the daily amount of living biomass which no longer participates in plant processes. Death rate of stems and roots is considered to be a function of development stage (see Figure 5.7.). This dependency is described using an AFGEN table with development stage as independent variable. Leaves death rate is more complicated. Leaf senescence due to shading (high LAI), water stress and also due to life span exceedance should be taken into account.
Stems and roots net growth rate can described by:
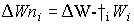 |
(5.43)
|
| where | DWni | : | Net dry matter growth rate of organ i | [kg ha-1 d-1] |
| DWi | : | Dry matter growth rate of organ i (see eq. 5.41) | [kg ha-1 d-1] | |
| Wi | : | Dry matter weight organ i | [kg ha-1] | |
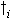 |
: | Death rate organ i | [kg kg-1 d-1] | |
| i | : | Stems (st), roots (rt) |
Stem and root death rates are crop specific and should be provided by the user. A dependency of development stage is assumed. AFGEN tables with development stage as independent variable are used to describe this dependency. Although the process that describes leaves death rate is more complicated than death rate calculation of stems and roots, establishing total dry weight of living leaves is similar to the computation of stems and roots dry matter weight. It can be found by integrating the net dry matter growth over time:
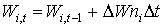 |
(5.44)
|
| where | Wi,t | : | Dry matter weight organ i at time step t | [kg ha-1] |
| DWni | : | Net dry matter growth rate of organ i | [kg ha-1 d-1] | |
| Dt | : | Time step | [d] | |
| i | : | Stems (st), roots (rt), leaves (lv) |
Equation (5.44) is recursive, the initial value for total crop dry matter weight
should be provided by the user, initial values of organ dry matter weight are
calculate: the initial crop dry matter weight is multiplied by the partioning
factors, pci, at emergence, yielding initial values of dry
weight of plant organs.
Growth of leaves
Area of green leaves is the major determinant for light absorption and photosynthesis. Under optimal conditions, light intensity and temperature are environmental factors influencing the leaf area expansion rate. Light intensity determines the photosynthesis rate and hence assimilates supply to the leaves. Temperature affects the rates of cell division and extension (Ng & Loomis, 1984; Sheehy et al., 1980; Acock et al., 1978). During the early stages of crop growth, temperature is the overriding factor. Leaf appearance rate and final leaf size are constrained by temperature through its effect on cell division and extension, rather than by assimilate supply (Hunt, 1982; Causton & Venus, 1981; van Dobben, 1962). The growth curve in the early stage has an exponential form. Some unpublished field data have shown that the exponential model should be restricted to the situation where the development stage, Ds,t < 0.3 and LAI < 0.75. In WOFOST/CGMS, however, it is assumed that the exponential growth rate of leaf area index is valid until the source-limited increase of leaf area index equals the exponential growth rate. Leaf area index growth rate per time step in the early, exponential growth stage can be calculated as:
 |
(5.45)
|
| where | Lexp,t | : | LAI growth rate at time step t during exponential growth stage | [ha ha-1 d-1] |
| RL | : | Maximum relative increase of leaf area index | [°C-1 d-1] | |
| Te | : | Daily effective temperature (see eq. 5.3c) | [°C] |
In theory, maximum relative increase of leaf area index, RL, is a function of effective temperature. For a relative wide range of temperatures RL responds more or less linearly to temperature (Hunt et al., 1985; Causton & Venus, 1981; van Dobben, 1962). In WOFOST/CGMS however, a fixed value per crop type is assumed, which should be given by the user. The accumulated leaf area index at time step t during the exponential growth stage can be described as:
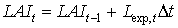 |
(5.46)
|
| where | Lexp,t | : | LAI growth rate at time step t during exponential growth stage | [ha ha-1 d-1] |
| Dt | : | Time step | [d] |
Equation (5.46) is recursive. LAIt is initialized by setting the starting value to the leaf area index at emergence. Leaf area index at emergence is crop specific and should be provided by the user. During crop development, leaf area expansion is increasingly restricted by assimilate supply (i.e. source limited increase). Branching and tillering generate an increasing number of sites per plant, where leaf initiation can take place. As mentioned earlier, it is assumed that the exponential growth rate of leaf area index will continue until it equals the source limited growth rate of the leaf area index. Leaf area index growth rate at time step t during the source limited growth stage can be described as:
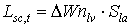 |
(5.47)
|
| where | Lsc,t | : | LAI growth rate at time step t during the source limited growth stage | [ha ha-1 d-1] |
| DWnlv | : | Net dry matter growth of leaves at time step t | [kg ha-1 d-1] | |
| Sla | : | Specific leaf area at time step t | [ha kg-1] |
Leaves net dry matter growth, DWnlv, can be found by subtracting weight of leaves that died during current time step from leaves dry matter growth, DWlv. This process will be described later in more detail in this paragraph. Specific leaf area, Sla, is defined as the increase of crop leaf area per kg weight increase of living leaves. Sla is crop specific and a function of development stage (see Figure 5.8.). An AFGEN table with development stage as independent variable is used to describe this dependency. The accumulated leaf area index at time step t during the source limited growth stage can be described as:
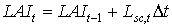 |
(5.48)
|
| where | Lsc,t | : | LAI growth rate at time step t during the source limited growth stage | [ha ha-1 d-1] |
| Dt | : | Time step | [d] |
Equation (5.48) is recursive. LAIt is initialized by setting the starting value equal to the leaf area index at emergence. The leaf area index at emergence is crop specific and should be provided by the user. In WOFOST/CGMS, however, accumulated leaf area cannot be calculated direct, leaf area index has to be corrected for leaf senescence which occurred during current time step. Leaf senescence can be caused by physiological ageing, water stress and/or high leaf area index (i.e. mutual shading). Later in this text, more attention will be paid to these effects. To correct for leaf senescence, specific leaf area of each time step, Sla, dry matter growth rate of leaves per time step, DWlv and the physiological age, Page (see eq. 5.52), have to be stored in three different arrays. These arrays are organized as follows: the first element of the arrays represents the most recent age class (or time step) and the last element of the arrays represents the oldest age class (or time step). It should be clear that the position of an element in the arrays represents its age class, in time steps. Dry matter weight of leaves, that have died during the current time step, has to be subtracted from the growth of dry matter weight per time step. One array contains thus the net dry matter growth of leaves per time step, DWnlv. The procedure which describes this process will be explained later in this text. After correction for leaf senescence, the accumulated leaf area can be established. Net dry matter weight of the leaves, DWnlv, in the remaining and new leaf classes is multiplied with the specific leaf areas (see eq. 5.47) to get the growth rate of the leaf area index of the living leaves per age class. Multiplication with Dt and summation over the classes yields the total leaf area index. The green area index of the stems and the storage organs is added to this amount. The total dry matter weight of living leaves can be found in a similar way by using equation (5.44).
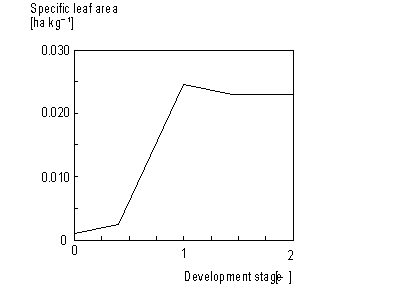
Figure 5.8. Specific leaf area as a function of development stage
As mentioned earlier, the green area index of stems and storage organs, may absorb a substantial amount of radiation and should therefore be added to the total leaf area index. Green area index of these organs can be calculated by:
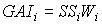 |
(5.49)
|
| where | GAIi | : | Green area index of organ i | [ha ha-1] |
| SSi | : | Specific green area of organ i | [ha kg-1] | |
| Wi | : | Dry matter organ i (see eq. 5.44) | [kg ha-1] | |
| i | : | Stems (st), storage organs (so) |
Specific green area of stems and storage organs are crop specific and should be provided by the user. Specific storage organ area is also known as the specific pod area. Special attention should be paid to the fact that during the exponential growth stage, specific leaf area is not established and for each time step the specific leaf area has to be calculated according to:
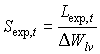 |
(5.50)
|
| where | Sexp,t | : | Specific leaf area at time step t during exponential growth stage | [ha kg-1] |
| DW lv | : | Leaves dry matter increase (see eq. 5.41) | [kg ha-1 d-1] | |
| Lexp,t | : | LAI growth rate at time step t during exponential growth stage (see eq. 5.46) | [ha ha-1 d-1] |
It is assumed that senescence does not occur during the exponential growing stage. This means that DWlv can be used in stead of the net dry matter growth, DWnlv.
Leaf senescence
As stated before, leaf senescence is more complicated. Senescence refers to:
- loss of capacity to carry out essential physiological processes
- loss of living biomass
Physiologic ageing
Leaves die due to exceedance of life span (i.e. physiologic ageing) which
is crop specific and is defined as the maximum time in days a leaf
can live at a constant temperature of 35°C.
The concept of lifespan is compatible with a definition in terms of
temperature sum as given by Gallagher (1979).The physiologic
ageing factor per time step can be calculated as:
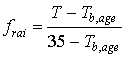 |
(5.51)
|
| where | frai | : | Physiologic ageing factor for leaf age increase | [-] |
| T | : | Daily (average) temperature | [°C] | |
| Tb,age | : | Lower threshold temperature for physiologic ageing | [°C] |
The lower threshold temperature for physiologic ageing, Tb,age, is crop specific and should be provided by the user. Integration of the physiologic ageing factor over time yields the physiologic age.
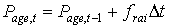 |
(5.52)
|
| where | Page,t | : | Physiologic age at time step t | [d] |
| frai | : | Physiologic ageing factor for leaf age increase | [-] | |
| Dt | : | time step | [d] |
Leaves may attain the age defined by the crop specific life span. However, as is mentioned earlier, they can not exceed it. In WOFOST/CGMS leaf age classes are checked; the first class younger than the defined life span become the oldest class. Note that death of old leaves takes place after ageing, being the result of the daily shifting from one leaf class to the next (Johnson & Thornley, 1983). In this way, life time of leaves is the maximum number of days that a leaf class contributes to the LAI and to photosynthesis.
Death rate due to water stress
Potential death rate of leaves due to water stress can be calculated
as:
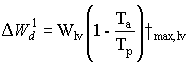 |
(5.53) |
| where | DW1d | : | Potential death rate of leaves due to water stress | [kg ha-1 d-1] |
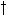 max,lv max,lv |
: | Maximum relative death rate of leaves due to water stress | [kg kg-1 d-1] | |
| Wlv | : | Leaves dry matter weight (see eq. 5.44) | [kg ha-1] | |
| Ta | : | Actual transpiration (see Subsection 6.1.) | [cm d-1] | |
| Tp | : | Potential transpiration (see Subsection 6.1.) | [cm d-1] |
Maximum relative death rate of leaves due to water stress,
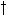 max,lv is crop specific and should
be provided by the user.
max,lv is crop specific and should
be provided by the user.
Death rate due to high leaf area index
Leaf senescence also occurs due to high leaf area index (i.e. mutual
shading). A relative death rate due to self-shading is defined which
increases linearly from zero at a certain, critical leaf area index, to
its maximum value at twice this critical leaf area index. Typical values
for the maximum relative death rate and the critical LAI are 0.03 d-1
and 4 ha ha-1, respectively (Spitters et al. 1989).
The potential death rate of leaves due to high LAI can be calculated as:
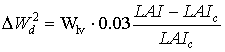 |
(5.54) |
| where | DW2d | : | Potential death rate of leaves due to high LAI | [kg ha-1 d-1] |
| Wlv | : | Dry matter weight of the leaves | [kg ha-1] | |
| LAI | : | Leaf area index | [ha ha-1] | |
| LAIc | : | Critical leaf area index | [ha ha-1] |
Critical leaf area index, LAIc, can be computed by:
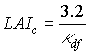 |
(5.55) |
| where | LAIc | : | Critical leaf area index | [ha ha-1] |
| kdf | : | Extinction coefficient for the diffuse radiation flux | [-] |
The last term of the right hand side of the equation 5.54 must be between 0 and 0.03. A value lower than 0 will be set to 0 and a value higher than 0.03 will be set to 0.03. WOFOST/CGMS selects the highest value of the two calculated potential death rates for further calculations of the reduction of dry matter weight increase of the leaf classes, per time step. Weight of leaves which have died during the current time step, can be calculated by multiplying death rate (due to water stress and/or high LAI), by the time step.
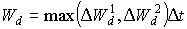 |
(5.56) |
| where | Wd | : | Weight of leaves that have died during current time step | [kg ha-1] |
| DW1d | : | Potential death rate of leaves due to water stress | [kg ha-1 d-1] | |
| DW2d | : | Potential death rate of leaves due to high LAI | [kg ha-1 d-1] | |
| Dt | : | Time step | [d] |
The weight of death leaves Wd is subtracted
from the weight of the oldest leaf class. If there is only one class the
result should be positive. When more leaf classes exist, the oldest leaf
class may be emptied completely, the remainder is subtracted from the next
leaf class. Emptying the oldest leaf class goes on, until the original
amount is dissipated completely and the remaining amount of leaves remains
positive. All leaves are shifted every time step (daily) to next class.
5.6. Root growth
Rate of vertical root extension is equal to the maximum daily increase, unless maximum rooting depth is reached. Transpiration by the vegetation must be balanced by water uptake from the soil. Water uptake depends on the difference in potential between water in the plant and in the soil. Resistance of transport of moisture from soil to atmosphere plays also an important role. Numerous experimental and theoretical studies have been conducted to determine the relative importance of various components of the total resistance (Newman, 1969a, 1969b; Andrews & Newman, 1969; Cowan, 1965; Slatyer & Gardner 1965; Gardner, 1960). The general consensus is that the major resistance to moisture transport is:- in the plant in case the soil moisture potential is low.
- in the soil in case the soil moisture potential is high.
crop specific
- Initial rooting depth, RDi
- Maximum rooting depth determined by the crop, RDcrop
- Maximum daily increase in rooting depth, RRmax
- Maximum rooting depth determined by the soil, RDsoil
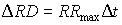 |
(5.57) |
| where | DRD | : | Increase of the rooting depth | [cm] |
| RRmax | : | Maximum daily increase in rooting depth | [cm d-1] | |
| Dt | : | Time step | [d] |
It is assumed that root extension growth continues until maximum rooting depth is reached. Rooting depth can be established by:
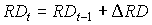 |
(5.58) |
| where | RDt | : | Rooting depth at time step t | [cm] |
| DRD | : | Increase of the rooting depth | [cm] |
Maximum rooting depth is established by taking the lowest value of the maximum rooting depth determined by the crop, RDcrop, maximum rooting depth determined by the soil, RDsoil, and the depth roots would reach in the potential production situation. It is assumed that maximum rooting depth is always equal or higher than initial rooting depth. In theory, root extension growth ceases when:
- no more assimilates are available
- an impermeable layer in the profile is reached
- the root tip reaches a soil compartment with a moisture content at or below wilting point (Salim et al., 1965)
- the root tip reaches the groundwater table
- when no more assimilates are available, in that case the simulation process ceases.
- when the root tip comes within ten centimeters of the groundwater table and the crop cannot form airducts. (The user should provide information if the crop can produce airducts or not.)
5.7. Crop variables
Crop species are characterized by a set of parameters and functions. In the following sub sections the estimated values, derived from experimental data, found in literature will be discussed in some detail.5.7.1. Distribution and absorption of light in the canopy
The radiation flux, incident on a leaf, is partly absorbed and partly scattered. Scattering consists of reflection and transmission. Species differ in optical properties of their leaves. A value of 0.20 is used for the scattering coefficient of individual leaves for PAR. Light distribution within the canopy is characterized by the extinction coefficient (k). As a reference, the situation is considered where leaves show a spherical angle distribution (i.e. as if they were placed on the surface area of a sphere), and are distributed randomly within the canopy volume. Assuming the above scattering coefficient of 0.20, the theoretical value of the extinction coefficient for the diffuse radiation flux is 0.72 (Goudriaan, 1977). Actual values, however, can deviate substantially from this theoretical value. Crops with more erect leaves have lower k values, whereas crops with more prostrate leaves show higher values of k. Here, a spherical leaf angle distribution is assumed. Alternative distributions can easily be implemented using the procedure described by Goudriaan (1988). A clustered leave distribution increases mutual shading, resulting in reduced light absorption and hence a lower value for k. However, especially in dicotyledons, new leaves are formed, preferably in gaps within the canopy, thus increasing the value of k. In WOFOST/CGMS the user should provide a value for the extinction coefficient for diffuse radiation (see eq. 5.12). The ratio between the user provided value and the theoretical value is used as a cluster factor (see eq. 5.13) which is subsequently used for calculation of the extinction coefficient of the direct component of direct radiation flux (see eq. 5.14) and the extinction coefficient of the total direct radiation flux (see eq. 5.15).Light absorption by organs other than leaves results in a calculated extinction coefficient which is too high, if the measured extinction is related to leaf area only. If light absorption and assimilation by these organs are important, as for ears and panicles in cereals, these processes should be accounted for explicitly; e.g. by treating them as light competing assimilators. This is also necessary for other factors, such as foliar diseases, that affect the photosynthetic capacity of the leaves and are distributed non-uniformly over canopy depth.
Typical values for k are 0.4 to 0.7 for monocotyledons and 0.65 to 1.1 for broad leaved dicotyledons (Monteith, 1969). The extinction coefficient can be estimated from measurements of PAR above and below a canopy with a known LAI, making sure that PAR is measured rather than total the global radiation.
The extinction coefficient has to be measured under a uniform overcast
sky and direct radiation has to be avoided as the solar elevation determines
the extinction coefficient for direct radiation. In the morning all direct
radiation will be absorbed and scattered in the top layer of the canopy
because of path length. At noon, direct radiation will penetrate further
in the canopy. If measurements have to be taken at a clear sky, a board
can be used to shade the light measurement instrument. Otherwise, the average
extinction coefficient over the day has to be calculated or the value has
to be corrected for solar elevation. Light extinction can be measured by
comparing radiation intensity above and below the canopy using a lightbar.
From the LAI and the measured light extinction, the extinction coefficient
for the diffuse flux can be calculated. When global radiation is measured
the extinction coefficient for the diffuse flux will be about 2/3 of the
extinction coefficient calculated for global radiation, because absorption
of near the infrared radiation by the canopy is less efficient.
An important factor which may confound the interpretation of measurements,
is the light absorption by other organs than leaves. When the extinction
coefficient for diffuse light is calculated from measurements, this effect should be
taken into account.
5.7.2. Photosynthesis-light response of individual leaves
The response of leaf photosynthesis to light intensity is characterized by its slope at low light intensity (e) and its maximum rate at light saturation (Am). With respect to the photosynthetic pathway, three groups of species can be identified: C3 and C4 species and CAM plants. Lists of C4 species have been published by Downton (1975) and Raghavendra & Das (1978).At a leaf temperature of 20°C, both C3 and C4 species have an initial light use efficiency of approximately 12.5 m g CO2 J-1 absorbed PAR or 0.45 kg CO2 ha-1 leaf h-1 (J m2 S-1)-1 (Ehleringer & Pearcy, 1983). In C3 species, e decreases with increasing temperature due to accelerated photo-respiration. This temperature effect is relatively small: e changes by about 1% with each change of 1°C in temperature (Farquhar et al., 1980; Ehleringer, 1978; Leverenz & Öquist, 1987). In C4 species, e is not affected by temperature because photo-respiration is suppressed. Among both C3 and C4 species, there is hardly any variation (Ehleringer & Pearcy, 1983). However, when e is expressed per unit of incident PAR, instead of per unit of absorbed PAR, apparent differences may occur, due to differences in the leaves absorption coefficient (Hunt et al., 1985). Yellowing of leaves results in increased reflection and transmission and, therefore, in an apparent decrease of e.
Measured values of leaves gross assimilation rate at light saturation (Am) show a large variation. The main sources of variation are differences in measurement conditions of temperature and ambient CO2 concentration, differences in physiological and anatomical leaves properties as a result of differences in leaf age, pre-treatment, and variation among species and cultivars.
Temperature influence on the leaf photosynthesis rate is described by multiplying the value of Am by a temperature-dependent factor. Relation between temperature and Am is based on Versteeg & van Keulen (1986). Various reaction types are distinguished according to crop species and habitat.
The photosynthetic capacity of leaves is affected by preceding conditions of radiation and temperature to which they were exposed: leaves adapt their photosynthetic capacity to the environment. Therefore, Am shows a seasonal course, which correlates with the time course of radiation and temperature (Parsons & Robson, 1981). As a consequence the photosynthetic characteristics of leaves of plants grown in climate rooms, are not representative for plants grown in the field. This adaptation may be mimicked by using a seven-day running average of Am values which have been adjusted for the environmental conditions (Schapendonk & Gaastra, 1984; Acock et al., 1978).
Photosynthetic capacity of a leaf is also affected by its age: Am reaches a maximum shortly after full leaf expansion, followed by a gradual decline with ageing (Rawson et al., 1983; Dwyer & Stewart, 1986). Differences in photosynthetic capacity of leaves are closely related to their nitrogen content, whether these variations are due to age, growing conditions or fertilizer application (van Keulen & Seligman, 1987). Leaves lower in the canopy have a lower photosynthetic capacity because they are older and are adapted to lower radiation levels (Acock et al., 1978; Williams, 1985). They also have lower nitrogen concentrations. The value of Am used in the model, refers to the photosynthetic capacity of full-grown leaves at the top of the canopy, as these leaves absorb most of the radiation. Effects of canopy senescence are introduced by a multiplication factor which is a function of development stage.
The photosynthetic capacity of leaves varies with crop species and cultivar.
The coefficient of variation in Am among genotypes within a
species is of the order of 5-10% (Spitters & Kramer, 1986). Species
can be grouped according to C3 and C4 types. Characteristic
values range from 15-50 kg CO2 ha-1 leaf
h-1 for C3 species and from 40-90 kg CO2
ha-1 h-1 for C4 species, depending on
leaf N concentration and temperature (Spitters et al., 1986). Other
values mentioned, range from 10-50 kg CO2 ha-1
leaf h-1 for C3 species and from 10-90 kg CO2
ha-1 h-1 for C4 species (Goudriaan, 1982;
van Keulen & Seligman, 1987). Species from ruderal habitats show higher
values than species from shaded habitats. In WOFOST/CGMS estimates of Am
are used which are found by fitting the exponential function (see eq.
5.20) to data of gross photosynthesis of individual leaves.
Such estimates may deviate from the measured values of photosynthetic
efficiency at low light and photosynthesis at light saturation. If no firmly
based value of Am is available, a value of 40 kg CO2 ha-1
h-1 for C3 species and 70 kg CO2 ha-1
h-1 for C4 species is, in general, a reasonable estimate.
5.7.3. Respiration
Respiration is usually measured as CO2 evolution in the absence of light energy. This dark respiration can be partitioned into growth and maintenance respiration. Estimation procedures have been reviewed by Amthor (1984). Standard values for maintenance coefficients are 0.03 for leaves, 0.015 for stems and 0.01 for roots (Spitters et al., 1989). For tropical crops lower values are used: 0.02 for the leaves and 0.01 for the other plant organs (Penning de Vries et al., 1989). As mentioned previously, these coefficients are affected by temperature, nitrogen content and mineral content of the plant tissue, and by the metabolic activity of the crop. Measured rates of dark respiration of full-grown leaves, showed a large variation among species and among cultivars (M.J. de Kock, Plant Research International, Wageningen, unpubl.). Maintenance coefficients applied in WOFOST/CGMS are not based on conclusive evidence. This introduces a significant uncertainty in simulating the crop growth rate, especially when the standing biomass is large compared to the current photosynthesis rate, as at the end of the growing period.hosted by Sudus Internet | powered by cmsGear
copyright 2025 Supit.net